Magik LC
Przedstawiam programik Magik LC, który jest tyle prosty, co uniwersalny. Wylicza elementy składowe obwodu rezonansowego LC szeregowego lub równoległego dla zadanych reaktancji obwodu (X1, X2) w dwóch punktach częstotliwościowych (f1, f2). Zanim podam przykłady zastosowania Magika LC, zapoznaj się z tabelką poniżej.
| f < frez | f > frez | |
| obwód szeregowy |
− |
+ |
| obwód równoległy |
+ |
− |
Omówimy zastosowanie programu Magik LC na konkretnych przykładach.
Filtr pasmowo-przepustowy
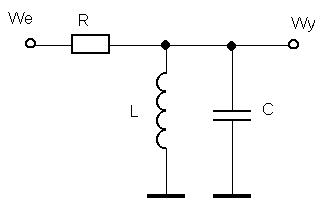
Chcemy wyliczyć filtr dla pasma CB 26.960–27.400 MHz. Kiedyś w latach 90-tych, w okresie świetności radia CB, nosiłem się z zamiarem wykonywania filtrów CB na zamówienie :-) Zakładamy R = 2 kΩ (wartość adekwatna bardziej dla zwykłego przestrojonego odbiornika). Dla spadku na krańcach pasma równym 3 dB, będziemy podawać reaktancje równe co do modułu wartości R. Wydruk z pracy programu daje:

Czyli otrzymujemy: L = 0.19 μH, C = 181 pF. Rozróżnianie znaków reaktancji przy jej zapodawaniu w istocie umiejscawia ją po odpowiedniej stronie częstotliwości rezonansowej obwodu (patrz tabelka). W praktyce dobieramy liczbę zwojów L tak, aby rezonans obwodu zmierzony rezonansomierzem wyniósł
![]() (1)
(1)
Czyli frez = 27.18 MHz. Ten sam wynik uzyskamy podając nie obie częstotliwości krańcowe, ale jedną krańcową i drugą rezonansową:

Reaktancję przy rezonansie X2 podałem względnie dużą w stosunku do 2 kΩ (znak tutaj jest nieistotny). Poniżej przedstawiam charakterystykę częstotliwościową obliczonego filtra.

Pułapka częstotliwościowa
Czasami zdarza się, że chcemy wyeliminować jakąś częstotliwość – stosujemy wtedy pułapkę częstotliwości.

W starych radioodbiornikach lampowych bywały tzw. eliminatory lokalnej stacji na falach długich. Z tyłu takiego odbiornika można było dokładnie nastawić częstotliwość f takiej pułapki. Innym przykładowym zastosowaniem pułapki f jest eliminator częstotliwości pośredniej na wejściu całego odbiornika radiowego. Dla przykładu chcę teraz wyeliminować częstotliwość pośrednią 9 MHz na wejściu odbiornika KF (krótkofalarskiego transceivera). Przyjmuję:
- R = 25 Ω jako równoległe połączenie Zwy anteny i Zwe odbiornika (50 Ω każda).
- Dolna f graniczna przy 3 dB tłumieniu np. 8.5 MHz.
Wyliczenie:

Czyli: L = 3.87 μH, C = 80.9 pF. Poniżej przedstawiam charakterystykę f tej pułapki.

We wszystkich przykładach można przyjąć w zadanej f inny niż 3 dB spadek transmitancji H. Ogólna zależność na reaktancję gałęzi równoległej (w powyższych przykładach były to obwody rezonansowe) jest następująca:
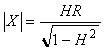 (2)
(2)
Poprzednio przyjmowaliśmy |X| = R, czyli H = 0.707 (−3 dB). Dla H = 0.5 (−6 dB) byłoby: |X| = 0.577 R.
Synteza filtra środkowo-przepustowego
Przeważnie w literaturze pojawiają się przepisy na wyliczenie filtrów dolno-przepustowych (FDP), pomijając filtry górno-przepustowe (FGP) i środkowo-przepustowe (FSP), względnie środkowo-zaporowe (FSZ). Jest to słuszne podejście, gdyż znając sposób liczenia FDP, można wyliczyć wszystkie inne np. FSP. Program Magik LC w wielu przypadkach to umożliwia.
Ogólna, zaprezentowana tutaj idea wyliczenia innego filtra, na podstawie FDP polega na:
- Pozyskaniu z FDP wartości reaktancji wszystkich gałęzi w punkach częstotliwości granicznych.
- Wyliczeniu elementów analogicznych gałęzi innego filtra na podstawie zdobytych reaktancji odpowiednich gałęzi FDP.
Przykładową syntezę przeprowadzę na FDP Butterwortha 3-go rzędu.
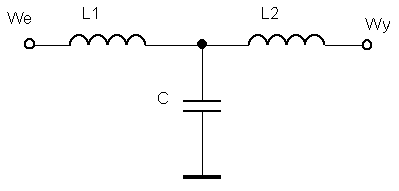
Dla górnej częstotliwości granicznej fg = 5 kHz i rezystancji obciążenia Robc = 1 kΩ wartości elementów wynoszą: L1 = 47.7 mH, L2 = 15.9 mH, C = 42.4 nF. Charakterystyka tego filtra przedstawia się następująco:

Teraz trzeba obliczyć reaktancje wszystkich gałęzi filtra przy f = fg = 5 kHz. Korzystamy ze wzorów:
![]() (3)
(3)
![]() (4)
(4)
Wyliczenia dają: XL1 =1499 Ω, XL2 = 499.5 Ω, XC = 750.7 Ω – filtr był liczony ze ścisłych wzorów matematycznych, tak więc domyślamy się dokładnej wartości poszczególnych X (efekt zaokrąglania, ale też wyrugowanie stałej π i "okrągła" wartość Robc). Podane wyżej wartości X zależą jedynie od rodzaju filtru (Czebyszewa, Butterwortha) i Robc – tak więc wartość fg mogła być zupełnie dowolna. Mamy więc już wszystkie dane, aby rozpocząć projektowanie FSP.
A jaki FSP zaprojektujemy? Niech to będzie np. filtr telegraficzny na pasmo 700–900 Hz. W zasadzie możnaby obliczenia przeprowadzić dla dowolnej Robc filtra stosując odpowiednie przeskalowanie wyliczonych X z FDP (zwykłe proporcje), jednak pozostaniemy przy Robc = 1 kΩ.
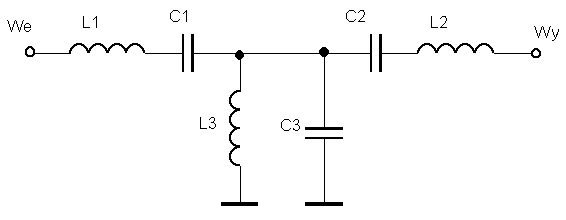
Obliczamy gałąź L1C1:

Czyli L1 = 1.19 H, C1 = 33.7 nF.
Gałąź L2C2:

Czyli L2 = 397 mH, C2 = 101 nF.
Gałąź L3C3:

Czyli L3 = 37.9 mH, C3 = 1.06 μF. Charakterystyka tak wyliczonego filtra przedstawia się następująco:
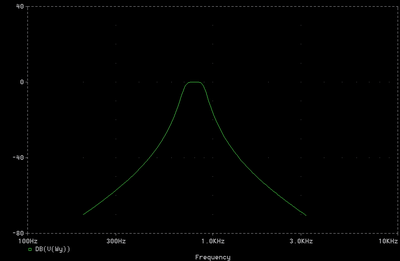
Gdybyśmy chcieli za pomocą programu Magik LC wyliczyć filtr górnoprzepustowy, wystarczyłoby jako fg zapodać jakąś niezwykle dużą wartość np. dla filtru na elementach dyskretnych byłoby to chociażby 1015. Następnie w wyniku należałoby pominąć te wartości L i C, aby pozostała struktura FGP.
I jeszcze jedna uwaga – pomijając ten punkt, generalnie częstotliwości f1 i f2 nie muszą leżeć po obu stronach frez lub jedna na frez. Należy jedynie zdawać sobie sprawę z kierunku opadania (narastania) X obwodu. Również może być f1 > f2. Jeśli tylko wyliczone L ≥ 0 i C ≥ 0, to taki obwód LC fizycznie istnieje.
Jeśli interesujesz się elektroakustyką, czytaj dalej.
Modyfikacja filtra głośnika wysokotonowego
Częstym problemem związanym z pracą głośnika wysokotonowego (głównie tubowych np. GDWT 9/80/5F) jest niedostateczne odfiltrowanie niższych częstotliwości jego pracy, co objawia się w postaci emitowania przez niego ze zbyt dużym natężeniem tonów leżących w pobliżu f rezonansowej (2.5 kHz dla wyżej wymienionego). Ma to głównie miejsce w przypadku, gdy chcemy "zejść" z fd filtra FGP dużo poniżej 8 kHz. Często zastosowanie FGP 2 rzędu jest wtedy niewystarczające. Obranie fd np. 6 kHz ma sens, gdyż możemy poprawić przetwarzanie pasma 6–8 kHz, ale musimy poprawić stromość filtra w najbliższym sąsiedztwie fd. Można zastosować filtr 3 rzędu (dodatkowa cewka i niestety naruszenie "zgrania" fazowego z FSP lub FDP) lub zmodyfikować posiadany filtr 2 rzędu ustawiając pułapkę na frez głośnika (tylko dodatkowy kondensator), co właśnie dalej uczynimy.
Zaprojektujemy FGP o dolnej częstotliwości granicznej fd = 6 kHz, z pułapką na frez głośnika. Stromość w paśmie frez–fd będzie większa niż w filtrze 2 rzędu, jednak dla f << frez tłumienie będzie gorsze niż przed modyfikacją FGP 2 rzędu. Przy czym frez = 2.5 kHz. Tłumienie (3 dB) i przesunięcie fazy (90°) przy fd będzie identyczne jak w filtrze 2 rzędu. Rezystancja obciążenia Robc = 8 Ω. Najpierw obliczamy zwykły filtr Butterwortha 2 rzędu.

Obliczenia dają: L = 300.1 μH, C = 2.345 μF.
Nasza modyfikacja, co jest istotne, będzie polegała jedynie na dodaniu kondensatora Cs w szereg z cewką L oraz zmianie liczby zwojów tej cewki. Powstanie wtedy pułapka f, której parametry musimy odpowiednio dobrać. Kondensator C pozostanie niezmieniony.

- Przy f = frez reaktancja pułapki musi wynieść: X = 0 Ω.
- Przy f = fd jej reaktancja pułapki musi być równa reaktancji cewki L przed modyfikacją: X = XL.
Z wyliczeń: XL = 11.31 Ω. Obliczenie L i Cs daje:

Czyli L = 363 μH, Cs = 11.2 μF. Wynika z tego konieczność dowinięcia niewielkiej liczby zwojów cewki L. Charakterystyki filtra przed i po modyfikacji przedstawiają się następująco:

Praktyczne próby odsłuchowe potwierdzają subiektywne odczucie lepszego wytłumienia rezonansu głośnika – mniejsze tłumienie zmodyfikowanego filtra ma miejsce dopiero na poziomie ogólnego tłumienia powyżej 20 dB.
Historia artykułu
2001: powstanie
2014: korekta po przejściu na Joomla (ostatni stat. HTML)
2023-12-11: dopiski i korekta po przejściu z J3 na J5
© Copyright Krzysztof Kolisz 2001