Radiotechnika

Synteza filtra środkowo-przepustowego

Przeważnie w literaturze pojawiają się przepisy na wyliczenie filtrów dolno-przepustowych (FDP), pomijając filtry górno-przepustowe (FGP) i środkowo-przepustowe (FSP), względnie środkowo-zaporowe (FSZ). Jest to słuszne podejście, gdyż znając sposób liczenia FDP, można wyliczyć wszystkie inne np. FSP. Program Magik LC w wielu przypadkach to umożliwia.

Ogólna, zaprezentowana tutaj idea wyliczenia innego filtra, na podstawie FDP polega na:

• Pozyskaniu z FDP wartości reaktancji wszystkich gałęzi w punkach częstotliwości granicznych.
• Wyliczeniu elementów analogicznych gałęzi innego filtra na podstawie zdobytych reaktancji odpowiednich gałęzi FDP.

Przykładową syntezę przeprowadzę na FDP Butterwortha 3-go rzędu.

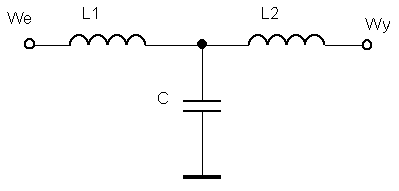
Dla górnej częstotliwości granicznej f_g = 5 kHz i rezystancji obciążenia R_obc = 1 kΩ wartości elementów wynoszą: L₁ = 47.7 mH, L₂ = 15.9 mH, C = 42.4 nF. Charakterystyka tego filtra przedstawia się następująco:

Teraz trzeba obliczyć reaktancje wszystkich gałęzi filtra przy f = f_g = 5 kHz. Korzystamy ze wzorów:

(3)

(4)

Wyliczenia dają: X_L1 =1499 Ω, X_L2 = 499.5 Ω, X_C = 750.7 Ω – filtr był liczony ze ścisłych wzorów matematycznych, tak więc domyślamy się dokładnej wartości poszczególnych X (efekt zaokrąglania, ale też wyrugowanie stałej π i "okrągła" wartość R_obc). Podane wyżej wartości X zależą jedynie od rodzaju filtru (Czebyszewa, Butterwortha) i R_obc – tak więc wartość f_g mogła być zupełnie dowolna. Mamy więc już wszystkie dane, aby rozpocząć projektowanie FSP.

A jaki FSP zaprojektujemy? Niech to będzie np. filtr telegraficzny na pasmo 700–900 Hz. W zasadzie możnaby obliczenia przeprowadzić dla dowolnej R_obc filtra stosując odpowiednie przeskalowanie wyliczonych X z FDP (zwykłe proporcje), jednak pozostaniemy przy R_obc = 1 kΩ.

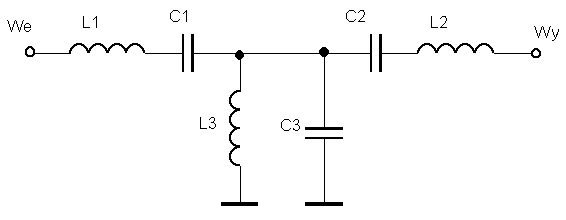
Obliczamy gałąź L₁C₁:

Czyli L₁ = 1.19 H, C₁ = 33.7 nF.

Gałąź L₂C₂:

Czyli L₂ = 397 mH, C₂ = 101 nF.

Gałąź L₃C₃:

Czyli L₃ = 37.9 mH, C₃ = 1.06 μF. Charakterystyka tak wyliczonego filtra przedstawia się następująco:

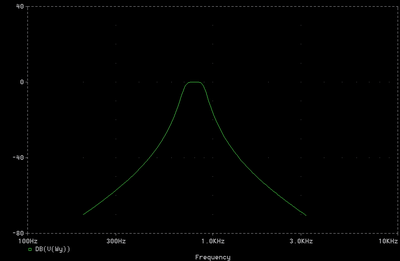
Gdybyśmy chcieli za pomocą programu Magik LC wyliczyć filtr górnoprzepustowy, wystarczyłoby jako f_g zapodać jakąś niezwykle dużą wartość np. dla filtru na elementach dyskretnych byłoby to chociażby 10¹⁵. Następnie w wyniku należałoby pominąć te wartości L i C, aby pozostała struktura FGP.

I jeszcze jedna uwaga – pomijając ten punkt, generalnie częstotliwości f₁ i f₂ nie muszą leżeć po obu stronach f_rez lub jedna na f_rez. Należy jedynie zdawać sobie sprawę z kierunku opadania (narastania) X obwodu. Również może być f₁ > f₂. Jeśli tylko wyliczone L ≥ 0 i C ≥ 0, to taki obwód LC fizycznie istnieje.

Jeśli interesujesz się elektroakustyką, czytaj dalej.