Praktyczna procedura projektowa
Jest ona niejako rozszerzeniem podstawowej procedury projektowej transformatora APTS2, umożliwiając pewniejszy start dla eksperymentatorów tego układu.
Zostanie tu uwzględniona indukcyjność rozproszenia $\boldsymbol{L_\textbf{rozpr}}$ transformatora niskotonowego TrN, przeniesiona na jego uzwojenie pierwotne. Tworzy ona wraz z $C_2$ pasożytniczy szeregowy obwód rezonansowy, pośrednio zniekształcający charakterystykę przenoszenia APTS2. Jak wyżej pokazałem (rys. 3), dla $\boldsymbol{R=5\textbf{ kΩ}}$ i $\boldsymbol{f_\textbf{p}=1\textbf{ kHz}}$, dopiero wartość $\boldsymbol{L_\textbf{rozpr}=50\textbf{ mH}}$ pozwala na osiągnięcie względnie liniowego przebiegu charakterystyki częstotliwościowej APTS2.
Przy dostatecznie małej $L_\text{rozpr}$ praktyczna procedura projektowa przekształca się w podstawową procedurę projektową.
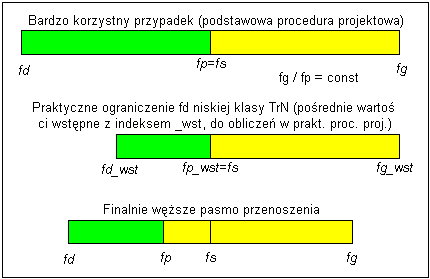
Zatem w praktyce, przyjmując podaną wyżej $f_\text{p}$, mamy ograniczenie na maksymalną indukcyjność uzwojenia pierwotnego TrN lub ogólniej, na maksymalną wartość stosunku $f_\text{p}/f_\text{d}$, który przy wcześniejszych założeniach oraz $L_\text{rozpr}=0$ wynosi $200$, lub maksymalną $f_\text{p}/f_\text{s}$ (gdzie $f_\text{s}$ jest docelowym geometrycznym środkiem pasma transformatora APTS2), który teoretycznie może się zwiększyć do wartości $1$. Ostatecznie po przeskalowaniu możemy osiągnąć węższe pasmo przenoszenia APTS2 niż w podstawowej procedurze projektowej (rys. 11).
Rys. 3 odnosi się do $R=5\text{ kΩ}$ i związanej z tym wartości $L_\text{rozpr}$. Pozostanie on niezmieniony (oraz poprawność działania całego układu) jeśli wraz ze zmianą $R$ zmienimy proporcjonalnie wszystkie rezystancje (włącznie z rezystancją drutu) i indukcyjności oraz odwrotnie proporcjonalnie pojemności.
Praktyczna procedura przedstawia się następująco:
1. Ustalenie ilorazu
$$k = {L_\text{pierw} \over L_\text{rozpr}} \tag{5}$$
dla danego typu transformatora TrN. Iloraz ten mówi nam ile razy indukcyjność pierwotna tego transformatora jest większa od indukcyjności rozproszenia przeniesionej na uzwojenie pierwotne. W moich pobieżnych pomiarach:
- $k=100$ dla transformatora sieciowego typu E,
- $k=500$ dla transformatora sieciowego toroidalnego.
- W transformatorach audio współczynnik $k$ jest rzędu co najmniej kilku tysięcy.
2. Obliczenie wstępne indukcyjności pierwotnej TrN
$$L_\text{pierw wst} = kL_\text{rozpr wst} \tag{6}$$
gdzie $\boldsymbol{L_\textbf{rozpr wst}=50\textbf{ mH}}$. Podana wartość $L_\text{rozpr wst}$ odnosi się do warunków rys. 3 i jest proporcjonalna do przyjętej $R$.
3. Wyliczenie wstępnej dolnej częstotliwości granicznej transformatora APTS2 (przy spadku $3\text{ dB}$)
$$f_\text{d wst} = {R \over 2\pi L_\text{pierw wst}} \tag{7}$$
gdzie $R$ jest rezystancją charakterystyczną APTS.
Ta wstępna wartość odnosi się do sytuacji przed przeskalowaniem względem przyjętej $f_\text{s}$.
4. Arbitralne wyznaczenie docelowego geometrycznego środka pasma $f_\text{s}$ transformatora APTS2 ($1\text{ kHz}$, jeśli korzystamy z wniosków rysunku 3).
5. Oszacowanie wstępnej górnej częstotliwości granicznej $f_\text{g wst}$ ($-3\text{ dB}$) transformatora APTS2 przy założeniu, że TrW pracuje od $\boldsymbol{2f_\textbf{s}=2f_\textbf{p wst}=2\textbf{ kHz}}$. Powyżej przyjmowałem przeciętne pasmo transformatora TrW, pozwalające sięgnąć $f_\text{g wst}=200\text{ kHz}$. Oszacowanie to opiera się na przeświadczeniu o minimalnych możliwościach naszego TrW.
6. Wyliczenie docelowych charakterystycznych częstotliwości transformatora APTS2 (przeskalowanie względem przyjętej $f_\text{s}$ wartości wstępnych):
$$f_\text{d} = {f_\text{s} \over \sqrt{f_\text{g wst} \over f_\text{d wst}}} \tag{8}$$
$$f_\text{g} = f_\text{s} \sqrt{f_\text{g wst} \over f_\text{d wst}} \tag{9}$$
$$f_\text{p} = f_\text{p wst} {f_\text{g} \over f_\text{g wst}} \tag{10}$$
Dalsze obliczenia będą się opierać już na przeskalowanych wartościach.
7. Obliczenie indukcyjności uzwojenia pierwotnego TrN wg. wzoru
$$L_\text{pierw} = {R \over 2\pi f_\text{d}} \tag{11}$$
Oczywiście należy mieć na uwadze konieczność przenoszenia przez TrN pasma do $f_\text{p}$. Gdyby tak nie było, co jest mało prawdopodobne, należy zmniejszyć indukcyjność wyliczoną w p.2 i powtórzyć obliczenia.
8. Obliczenie $L$ i $C$ wg. (1) i (2). Przypominam, że $L$ jest indukcyjnością uzwojenia pierwotnego TrW.
9. Rozłożenie pojemności $C$ na $C_1$ i $C_2$ wg. (3) i (4).
Już w tym miejscu należy oszacować, czy wskutek zastosowania TrN o bardzo dużym $k$ pojemność jego uzwojenia pierwotnego nie przekroczy $C_1$. Jeśli przekroczy (co jest mało prawdopodobne), należy zmniejszyć indukcyjność wyliczoną w p.2 i powtórzyć obliczenia.
10. Obliczenie uzwojeń wtórnych składowych transformatorów z zachowaniem równości obu przekładni.