Wszechprzepustowy transformator szeregowy APTS

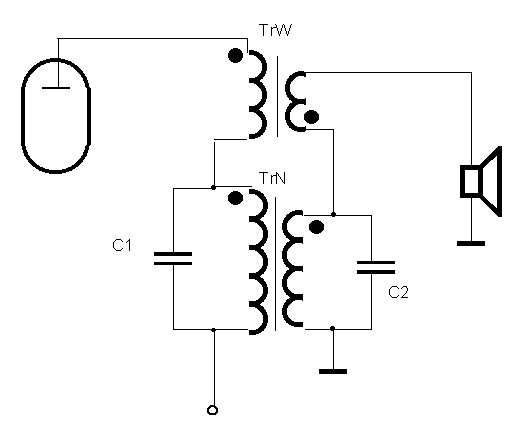
Prezentowany układ wszechprzepustowego transformatora szeregowego APTS (all-pass transformer / series, rys. 1) realizuje podział całego pasma częstotliwości na podzakresy, w przypadku APTS2 dolny (niskotonowy) i górny (wysokotonowy), które transformowane są oddzielnie przez każdy z transformatorów składowych. APTS wydaje się konkurencyjny w stosunku do jednego transformatora szerokopasmowego, przy założeniu nie pobierania ujemnego sprzężenia zwrotnego (USZ) zza transformatorów. Pomijając ograniczenia pasma, w istocie układ ten jest bowiem wszechprzepustowym filtrem 1-⁠go rzędu APF1 (all-⁠pass filter), co jest tutaj cechą niepożądaną.

APTS można więc stosować jako transformator w.cz., na przykład antenowy, a nawet transformator wyjściowy wzmacniacza lampowego m.cz. (USZ z anody lampy).

Obecnie przedstawiam jedynie opis teoretyczny, gdyż dotychczasowe praktyczne testy (APTS2) w akustycznym wzmacniaczu lampowym nie były na tyle regularne, aby ich opis można było tutaj zamieścić – zrealizowałem je na dość przypadkowych elementach, a samą ocenę dokonałem na słuch. Wyniki jednak były bardzo zachęcające. Ponadto wykonałem gruntowną symulację komputerową APTS2, która pokazała wszystkie szczegóły i uwarunkowania działania układu.

Analiza teoretyczna

Zbudujmy model APTS składający się z dwóch transformatorów, czyli APTS2 (rys. A2).

Warunkiem wstępnym jest równość przekładni obu transformatorów. W celu wyeliminowania zjawisk nie będących przedmiotem analizy, dokonajmy następujących uproszczeń:

• Przekładnie obu składowych transformatorów $n_\text{n}=n_\text{w}=n=1$, gdzie $n=z_2/z_1$ i $z_1$ – liczba zwojów uzwojenia pierwotnego, a $z_2$ – wtórnego. Oczywiście w ogólnym przypadku $n^2=R_\text{o}/R_\text{g}$.
• Współczynniki sprzężenia pomiędzy uzwojeniami pierwotnym i wtórnym obu transformatorów są równe 1.
• Pojemności wejściowa i wyjściowa transformatora niskotonowego TrN są skupione na jego uzwojeniu pierwotnym.
• W dalszej części wyeliminujemy dolne ograniczenie pasma przenoszenia układu.

Transmitancja napięciowa modelu APTS2 (rys. A2) opisana jako wzmocnienie transmisyjne napięć przedstawia się następująco

$$T_1(s) = {u_\text{wy}(s) \over e_\text{g}(s)} = {-R_\text{o}L_\text{n}L_\text{w}Cs^3+R_\text{o}(L_\text{n}-L_\text{w})s \over (R_\text{g}+R_\text{o})L_\text{n}L_\text{w}Cs^3+(R_\text{g}R_\text{o}C+4L_\text{w})L_\text{n}s^2+(R_\text{g}+R_\text{o})(L_\text{n}+L_\text{w})s+R_\text{g}R_\text{o}}\tag{B1}$$

gdzie $s=\mathrm{j}\omega$ jest zmienną zespoloną, tutaj ograniczoną do osi urojonej (widma).

W celu eliminacji ograniczenia pasma przenoszenia od strony najniższych częstotliwości, zostanie znacznie zwiększona wartość indukcyjności $L_\text{n}$

$$T_2(s) = \lim_{L_\text{n} \to \infty}T_1(s) = {-R_\text{o}L_\text{w}Cs^2+R_\text{o} \over (R_\text{g}+R_\text{o})L_\text{w}Cs^2+(R_\text{g}R_\text{o}C+4L_\text{w})s+R_\text{g}+R_\text{o}}\tag{B2}$$

W ten sposób wpływ tej indukcyjności został w dalszej analizie zlikwidowany tzn. nasz model przenosi teraz nawet składową stałą. Zauważmy, że dla $\omega=0$ transmitancja (B2) wynosi ${R_\text{o} \over R_\text{g}+R_\text{o}}$ (patrz wyrazy wolne w liczniku i mianowniku), natomiast dla $\omega\to\infty$ transmitancja ta zmierza do ${-R_\text{o} \over R_\text{g}+R_\text{o}}$ (przeciwfaza, patrz współczynniki przy $s^2$). Mamy więc potwierdzenie, że APTS2 jest filtrem APF1, co wynika z odwróconego połączenia uzwojeń wtórnych transformatorów składowych.

Teraz interesować nas będzie uzyskanie w modelu APTS2 stałości jedynie modułu $|T_2(\omega)|$ (niezależnie od $\omega$), gdyż z faktu, że jest on filtrem APF1 wynika niemożność uzyskania stałości fazy.

$$|T_2(\omega)| = {R_\text{o}L_\text{w}C\omega^2+R_\text{o} \over \sqrt{(R_\text{g}+R_\text{o})^2L_\text{w}^2C^2\omega^4+[R_\text{g}^2R_\text{o}^2C^2-2(R_\text{g}-R_\text{o})^2L_\text{w}C+16L_\text{w}^2]\omega^2+(R_\text{g}+R_\text{o})^2}}\tag{B3}$$

Do przeanalizowania przebiegu $|T_2(\omega)|$ potrzebna nam będzie pochodna tej funkcji względem pulsacji $\omega$

$${\mathrm{d}|T_2(\omega)| \over \mathrm{d}\omega} = {R_\text{o}(R_\text{g}^2C-4L_\text{w})(R_\text{o}^2C-4L_\text{w})(L_\text{w}C\omega^2-1)\omega \over \lbrace\sqrt{(R_\text{g}+R_\text{o})^2L_\text{w}^2C^2\omega^4+[R_\text{g}^2R_\text{o}^2C^2-2(R_\text{g}-R_\text{o})^2L_\text{w}C+16L_\text{w}^2]\omega^2+(R_\text{g}+R_\text{o})^2}\rbrace^3}\tag{B4}$$

Warunkiem uzyskania stałości funkcji $|T_2(\omega)|$ jest występująca dla każdej wartości $\omega$ równość

$${\mathrm{d}|T_2(\omega)| \over \mathrm{d}\omega} = 0 \tag{B5}$$

Ogólnym, mającym fizyczny sens rozwiązaniem równania (B5) jest spełnienie przynajmniej jednej z trzech poniższych równości

$$C = {4L_\text{w} \over R_\text{g}^2} \tag{B6}$$

$$C = {4L_\text{w} \over R_\text{o}^2} \tag{B7}$$

$$\omega^2 = {1 \over L_\text{w}C} \tag{B8}$$

Wyrażenia (B6) i (B7) są interesującymi nas rozwiązaniami, gdyż nie zależą od $\omega$. Na ich podstawie definiujemy rezystancję charakterystyczną $\boldsymbol{R}$ transformatora APTS (rys. A2)

$$\boxed{R \stackrel{\text{def}}{=} 2\sqrt{L_\text{w} \over C}} \tag{B9}$$

Rozwiązanie (B8) informuje nas o istnieniu jednego ekstremum funkcji $|T_2(\omega)|$, które oczywiście zanika przy spełnieniu równania (B6) lub (B7). Występuje ono na pulsacji rezonansowej szeregowego obwodu rezonansowego $L_\text{w}C$. Nazwijmy pulsację występowania tego w zasadzie potencjalnego ekstremum pulsacją podziału $\boldsymbol{\omega_\textbf{p}}$ transformatora APTS, jako że występuje w tym punkcie równomierny podział napięcia pomiędzy oboma transformatorami składowymi

$$\boxed{\omega_\text{p} = {1 \over \sqrt{L_\text{w}C}}} \tag{B10}$$

Ostatecznie na podstawie (B9) i (B10) otrzymujemy  wzory projektowe transformatora APTS

$$\boxed{L_\text{w} = {R \over 2\omega_\text{p}}} \tag{B11}$$

$$\boxed{C = {2 \over \omega_\text{p}R}} \tag{B12}$$

Z (B6), (B7) i (B9) wynika warunek stałości $|T_2(\omega)|$. Wystarczy spełnić jedną z następujących dwóch równości lub inaczej – warunków dopasowania

$$\boxed{R_\text{g} = R} \tag{B13}$$

$$\boxed{R_\text{o} = R} \tag{B14}$$

Wtedy to niezależnie od $\omega$ moduł transmitancji APTS2 będzie równy (rys. A3 i A4)

$$|T_2(\omega)| = {R_\text{o} \over R_\text{g}+R_\text{o}} = \mathrm{const} \tag{B15}$$

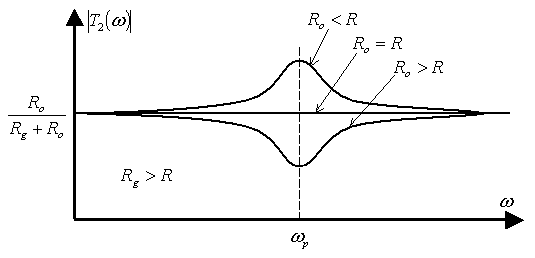
Analiza przebiegu modułu impedancji wejściowej $|Z_\text{we}(\omega)|$ "widzianej" na prawo od $R_\text{g}$ (rys. A2 i A5) pokazuje, że jest ona niezależna od $\omega$ jedynie przy $R_\text{o}=R$. Impedancja ta ma wtedy charakter rezystancji i jest równa $R$. Przy dowolnych wartościach $R_\text{o}$ impedancja wejściowa $Z_\text{we}(\omega_\text{p})$ transformatora APTS2 przypomina impedancję wejściową ćwierćfalowej linii długiej – jest odwrotnością $R_\text{o}$ względem $R$ zawsze mając charakter rezystancyjny.

Ostatecznie, ze względu na możliwość wahań rezystancji $R_\text{o}$, korzystnie jest przyjąć mocniejszą zasadę

$$R_\text{g} = R = R_\text{o} \tag{B16}$$

To niezwykłe zachowanie się APTS2 na rys. A4 i A5 przy $\omega=\omega_\text{p}$ można wytłumaczyć transformacyjnymi właściwościami szeregowego obwodu rezonansowego $L_\text{w}C$. W szczególności przebieg $|Z_\text{we}(\omega)|$ (im mniejsza $R_\text{o}$ tym większy $|Z_\text{we}(\omega_\text{p})|$) można wyjaśnić następująco: niska rezystancja $R_\text{o}$ przytłumia szeregowy obwód  rezonansowy $L_\text{w}C$, nie pozwalając mu na osiągnięcie "w pełni" rezonansu (dużej dobroci $Q$), a tym samym zera omów na jego wejściu.

Analizując wpływ dokonanych na wstępie uproszczeń, w celu powrotu do praktycznego schematu APTS2 z rys. 1 trzeba wymienić:

• Przyjmując przekładnie transformatorów $n_\text{n}=n_\text{w}=n\neq 1$, zamiast $R_\text{o}$ we wzorach trzeba wstawić $R_\text{o}'={R_\text{o}\over n^2}$ ($R_\text{o}$ przeniesione na wejście). Stosownie do przekładni $n$ ulegają zmianie indukcyjności uzwojeń wtórnych obu transformatorów składowych. Dodatkowo, jeśli naruszymy warunek $n_\text{n}=n_\text{w}$, zostanie zdeformowana charakterystyka przenoszenia APTS2.

• Rozkładając pojemność $C$ na dwie $C_1$ i $C_2$ wydaje się najkorzystniejszym dokonać równego podziału na jednakowe reaktancje względne po obu stronach TrN tzn. $C_1={C\over2}$, $C_2={C\over2n^2}$. To zalecenie ma jednak naturę tylko praktyczną.

• Przyjmując skończoną wartość $L_\text{n}$, trzeba zapewnić pojemność zastępczą równoległego obwodu rezonansowego $L_\text{n}C_\text{n}$ (gdzie $C_\text{n}$ są pojemnościami „wlutowanymi” oraz uzwojeń, przeniesionymi na wejście TrN) przy $\omega_\text{p}$ zbliżoną do $C$. Jednak w praktyce wpływ ten jest względnie mały.

Dogłębne omówienie

Przyjrzyjmy się dokładniej pracy APTS2 w kontekście lampowego wzmacniacza małej częstotliwości.

W układzie tym $R_\text{g}$ jest rezystancją wewnętrzną lampy głośnikowej, często oznaczaną przez $\varrho$. W przypadku triody $R_\text{g}$ wynosi kilka kΩ będąc w przybliżeniu równą jej optymalnej rezystancji obciążenia. W przypadku pentody $R_\text{g}$ jest bardzo duża, rzędu setek kΩ i więcej, co czyni tę lampę niemal idealnym źródłem prądowym. Z punktu widzenia każdego transformatora głośnikowego, w tym APTS, wartość $R_\text{g}$ pentody jest praktycznie nieskończenie duża. Jednak pobierając ujemne sprzężenie zwrotne (USZ) z anody tej lampy można znacznie zmniejszyć jej $R_\text{g}$ np. do poziomu $R$. Rezystancja $R_\text{o}$ jest natomiast rezystancją głośnika. Oczywiście jest to spore uproszczenie, gdyż rzadko w którym punkcie częstotliwości głośnik reprezentuje sobą na wejściu czystą rezystancję.

W dalszym ciągu jako znamionowe przyjmujemy: $\boldsymbol{R_\textbf{g}=R=5\textbf{ kΩ}}$ i $\boldsymbol{R_\textbf{o}=8\textbf{ Ω}}$. Daje nam to przekładnię APTS wynoszącą $\boldsymbol{n=1/25}$.

Wszechprzepustowy transformator szeregowy APTS2, jako będący filtrem APF1 wprowadza zniekształcenia fazy (rys. 2) tzn. bardzo łagodne przejście od 0° do −180°. Spowodowane jest to odwróconym połączeniem uzwojeń wtórnych transformatorów składowych. Pociąga to za sobą niemożność załączenia USZ z wyjścia APTS. Takie połączenie tych uzwojeń jest jednak konieczne w celu eliminacji niekorzystnych skutków rezonansu szeregowego uzwojenia pierwotnego TrW i pojemności $C_1$ (i transformowanej $C_2$). Rezonans ten powodował powstawanie dużej doliny w okolicy częstotliwości podziału $f_\text{p}$.

W najprostszym modelu zastępczym możemy sobie bowiem wyobrazić sytuację równoległego połączenia najprostszego filtra dolnoprzepustowego L-R z najprostszym filtrem górnoprzepustowym C-R. W rezultacie otrzymamy filtr LC-R będący równoległym obwodem rezonansowym (pułapką częstotliwości) zasilającym rezystor obciążenia $R/2$. Odwrócenie fazy jednego z tych filtrów pozwala w prosty sposób rozwiązać ten problem. W przypadku APTS2 trzeba ponadto rozsunąć zakresy pracy obu transformatorów składowych, aby zlikwidować szczyt na wykresie. To wszystko odbywa się jednak kosztem stałości fazy.

Jak wspomniałem, APTS2 jest wszechprzepustowym filtrem APF1 (pomijając ograniczone pasmo częstotliwości rzeczywistego APTS), którego transmitancja niestety nie jest odwracalna (nie jest możliwe "wyprostowanie" fazy) przy pomocy jakiegokolwiek przyczynowego obiektu dołączonego na wyjście układu. Do takich przyczynowych obiektów zaliczamy wszelaką elektronikę analogową np. obwody pasywne RLC, czy filtry aktywne.

Warunkiem poprawnej pracy APTS2 jest bardzo mała indukcyjność rozproszenia TrN, co niejako koliduje z głównym założeniem zastosowania tanich transformatorów (rys. 3). Indukcyjność ta wraz z $C_2$ tworzy pasożytniczy szeregowy obwód rezonansowy, który pośrednio wpływa na charakterystykę częstotliwościową układu.

Rezystancja drutu nawojowego ma istotny wpływ na wielkość "szkody" wyrządzonej przez indukcyjność rozproszenia TrN. Większa wartość tej rezystancji osłabia niekorzystne oddziaływanie tej indukcyjności. Oczywiście zwiększają się wtedy straty mocy, ale inna symulacja komputerowa pokazuje, że istnieje optymalna wartość rezystancji drutu, przy której "korzyść znacznie przewyższa straty" – mniej więcej pokrywa się ona z rzeczywistą rezystancją drutu nawojowego.

Warto też zwrócić uwagę na fakt, że mogące wystąpić z tytułu indukcyjności rozproszenia TrN zafalowania charakterystyki są względnie wąskopasmowe i w praktyce mogą okazać się mało istotne lub po prostu zostać "rozmyte" w rzeczywistych transformatorach, gdzie indukcyjności i pojemności są bardziej rozłożone niż w analizowanym modelu.

Jeśli nie zaznaczę inaczej, będę pomijał wpływ indukcyjności rozproszenia TrN.

Rozdział częstotliwości w APTS2 następuje na uzwojeniach TrW (indukcyjności ściśle określone) oraz pojemnościach $\boldsymbol{C_1}$ i $\boldsymbol{C_2}$ (również określone). Jak dalej pokażę, z ich wartościami jest związana  rezystancja charakterystyczna $\boldsymbol{R}$ transformatora APTS, której sens jest podobny do impedancji falowej filtru. Jeśli przynajmniej jedna z wielkości: $\boldsymbol{R_\textbf{g}}$ lub $\boldsymbol{R_\textbf{o}}$ (przetransformowana) jest równa $\boldsymbol{R}$, otrzymujemy liniowy przebieg charakterystyki przenoszenia w okolicy $\boldsymbol{f_\textbf{p}}$.

Poniżej przedstawiam tę sytuację (rys. 4, 5 i 6). Każdy wykres pokazuje przebieg $\boldsymbol{U_\textbf{wy}(f)}$ całości APTS2 w zależności od $\boldsymbol{R_\textbf{g}}$. Istotny jest tu tylko fragment w okolicy $\boldsymbol{f_\textbf{p}=1\textbf{ kHz}}$. Mamy źródło prądowe $I$ (lampa głośnikowa) o wartości 20 mA i zwieramy je kolejno rezystancjami 1 kΩ, 3 kΩ, 5 kΩ, ..., 25 kΩ z krokiem 2 kΩ (kolejne krzywe od dołu), co ma symulować różne $R_\text{g}$. Załączając te rezystancje na wyjście źródła $I$ powodujemy oczywiście zmianę wartości napięcia wyjściowego lampy i dalej APTS2, ale wydaje się to akurat tutaj nie przeszkadzać.

Transformatory składowe APTS2 przekładają znamionową rezystancję głośnika $R_\text{o}$ z 8 Ω na 5 kΩ. Trzeci przebieg od dołu przedstawia sytuację przy $R_\text{g}=R$.

Na rys. 4, ze względu na równość ${R_\text{o} \over n^2}=R$, nawet przy $R_\text{g}\to\infty$ (sytuacja podobna do pentody, nie uwidoczniona na rysunku) uzyskujemy równomierny przebieg.

Kolejne rys. 5 i 6 pokazują przebiegi przy innych rezystancjach głośnika $R_\text{o}$: 16 i 4 Ω. Widać, że tylko przy $\boldsymbol{R_\textbf{g}=R}$ (3-ci przebieg od dołu) mamy całkowitą niezależność charakterystyki w pobliżu $f_\text{p}$ od rezystancji głośnika.

To dziwne zachowanie się transformatora APTS2 wynika ze wspomnianego na początku rezonansu szeregowego $L_\text{w}C$.

Na rys. 7 widać kolejną dziwną rzecz – im mniejsza rezystancja głośnika, tym mniejszy spadek $\boldsymbol{U_\textbf{we}}$ transformatora APTS2 przy $\boldsymbol{f=f_\textbf{p}}$. Wytłumaczenie jest proste – niska rezystancja głośnika bardziej przytłumia szeregowy obwód rezonansowy $L_\text{w}C$, nie pozwalając mu tym samym na osiągnięcie w "pełni" rezonansu (dużej dobroci $Q$), czyli zera omów na wejściu APTS2. Wykres ten, ale dla $U_\text{wy}$, przedstawiałby oczywiście 3 linie proste (patrz poprzednie wykresy).

Ostatecznie wg. rysunków 4–7, zalecam zachowanie warunku

$$\boldsymbol{R_\textbf{g} = R = {R_\textbf{o} \over n^2}}$$

Najodpowiedniejsza wydaje się więc tutaj trioda mająca $R_\text{g}$ porównywalną z optymalną rezystancją obciążenia tej lampy. Oczywiście można zastosować z takim samym skutkiem pentodę + USZ (pobrane np. z anody), które to sprzężenie pozwoli jej osiągnąć niższą (docelową) $R_\text{g}$.

Na rys. 8 widzimy, że modelowy rezonans szeregowy $L_\text{w}C$ nie powoduje żadnych przepięć na składowych transformatorach. Dalej pokażę, że rezonans ten ma miejsce przy małej dobroci i nie powoduje żadnych oscylacji w APTS2.

Przyjmując dla każdego składowego transformatora $f_\text{g}/f_\text{d}=100$ (−3 dB), można by w APTS2 z łatwością osiągnąć pasmo 10 Hz – 100 kHz. Ale transformator APTS2 zapewnia dużo szersze pasmo, niż suma pasm transformatorów składowych! (wszystko to przy założeniu małej indukcyjności rozproszenia TrN). Wynika to z możliwości większego niż mogłoby się wydawać rozstawienia pasm obu transformatorów, gdyż w okolicy $f_\text{p}$ niejako "wspomagają" się nawzajem (sumowanie w fazie) za sprawą wspomnianego szeregowego obwodu rezonansowego ($L_\text{w}$ i pojemności uzwojeń TrN reprezentowanych przez $C$). Obwód ten nie wprowadza jednak żadnych oscylacji (potencjalnie na $f_\text{p}$), gdyż pracuje w warunkach małej dobroci (rys. 9 i 10).

W zamian braku możliwości objęcia przez USZ transformatora APTS2, jest korzyść podziału całego pasma na podzakresy, co z pewnością przyczyni się do zmniejszenia zniekształceń nieliniowych wnoszonych przez transformatory składowe.

Podstawowa procedura projektowa

Nie uwzględnia ona istnienia indukcyjności rozproszenia uzwojenia pierwotnego transformatora niskotonowego TrN.

1. Obieramy częstotliwość podziału $f_\text{p}$.

2. Obliczamy indukcyjność uzwojenia pierwotnego transformatora wysokotonowego TrW oraz pojemność widzianą na zaciskach uzwojenia pierwotnego TrN wg. wzorów (porównaj z (B11) i (B12))

$$L = {R \over 4\pi f_\text{p}} \tag{1}$$

$$C = {1 \over \pi f_\text{p}R} \tag{2}$$

gdzie:
$R$ – rezystancja charakterystyczna transformatora APTS,
$f_\text{p}$ – częstotliwość podziału pomiędzy oboma transformatorami składowymi.

Przykładowo, dla $\boldsymbol{f_\textbf{p}=1\textbf{ kHz}}$ i $\boldsymbol{R=5\textbf{ kΩ}}$ mamy $\boldsymbol{L=398\textbf{ mH}}$ i $\boldsymbol{C=63.7\textbf{ nF}}$.

Można tu oszacować dodatkowy zysk szerokości pasma wynoszący... 2 oktawy (!) w stosunku do sumy pasm obu składowych transformatorów (tę zależność widać bezpośrednio we wzorach (1) i (2)). Ostatecznie można przyjąć dla dwóch składowych transformatorów o $f_\text{g}/f_\text{d}=100$ każdy, pasmo przenoszenia transformatora APTS2 równe np. 5 Hz – 200 kHz (−3 dB)! Wszystko to przy założeniu małej indukcyjności rozproszenia TrN.

Problemem pozostaje kwestia "rozbicia" pojemności $C$ na $C_1$ i $C_2$. Wydaje się, że najlepszym rozwiązaniem będzie podział na dwie równe reaktancje względne po obu stronach TrN (względem np. 5 kΩ i 8 Ω). Przykładowo

$$C_1 = {C \over 2} \tag{3}$$

$$C_2 = {C \over 2n^2} \tag{4}$$

$\boldsymbol{C_1=31.9\textbf{ nF}}$, $\boldsymbol{C_2=19.9\textbf{ µF}}$.

3. Wyznaczenie indukcyjności uzwojenia pierwotnego TrN odbywa się na podstawie znajomości $C_1$. Ideałem byłoby, aby pojemność uzwojenia pierwotnego TrN była równa właśnie $C_1$ – uzyskamy wtedy najszersze pasmo od dołu (z założenia indukcyjność rozproszenia do pominięcia). Jednak w praktyce z pewnością pojemność uzwojenia będzie musiała być mniejsza, a brakującą część do $C_1$, trzeba będzie uzupełnić kondensatorem zewnętrznym. $C_2$ montujemy od razu – pojemności uzwojenia wtórnego są pomijalnie małe.

4. Uzwojenia wtórne TrN i TrW obliczamy na podstawie ogólnie znanych zależności pamiętając, aby przekładnie obu składowych transformatorów były sobie równe.

Praktyczna procedura projektowa

Jest ona niejako rozszerzeniem podstawowej procedury projektowej transformatora APTS2, umożliwiając pewniejszy start dla eksperymentatorów tego układu.

Zostanie tu uwzględniona indukcyjność rozproszenia $\boldsymbol{L_\textbf{rozpr}}$ transformatora niskotonowego TrN, przeniesiona na jego uzwojenie pierwotne. Tworzy ona wraz z $C_2$ pasożytniczy szeregowy obwód rezonansowy, pośrednio zniekształcający charakterystykę przenoszenia APTS2. Jak wyżej pokazałem (rys. 3), dla $\boldsymbol{R=5\textbf{ kΩ}}$ i $\boldsymbol{f_\textbf{p}=1\textbf{ kHz}}$, dopiero wartość $\boldsymbol{L_\textbf{rozpr}=50\textbf{ mH}}$ pozwala na osiągnięcie względnie liniowego przebiegu charakterystyki częstotliwościowej APTS2.

Przy dostatecznie małej $L_\text{rozpr}$ praktyczna procedura projektowa przekształca się w podstawową procedurę projektową.

Zatem w praktyce, przyjmując podaną wyżej $f_\text{p}$, mamy ograniczenie na maksymalną indukcyjność uzwojenia pierwotnego TrN lub ogólniej, na maksymalną wartość stosunku $f_\text{p}/f_\text{d}$, który przy wcześniejszych założeniach oraz $L_\text{rozpr}=0$ wynosi 200, lub maksymalną $f_\text{p}/f_\text{s}$ (gdzie $f_\text{s}$ jest docelowym geometrycznym środkiem pasma transformatora APTS2), który teoretycznie może się zwiększyć do wartości 1. Ostatecznie po przeskalowaniu możemy osiągnąć węższe pasmo przenoszenia APTS2 niż w podstawowej procedurze projektowej (rys. 11).

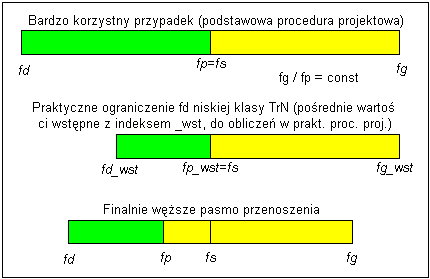
Rys. 3 odnosi się do $R=5\text{ kΩ}$ i związanej z tym wartości $L_\text{rozpr}$. Pozostanie on niezmieniony (oraz poprawność działania całego układu) jeśli wraz ze zmianą $R$ zmienimy proporcjonalnie wszystkie rezystancje (włącznie z rezystancją drutu) i indukcyjności oraz odwrotnie proporcjonalnie pojemności.

Praktyczna procedura przedstawia się następująco:

1. Ustalenie ilorazu

$$k = {L_\text{pierw} \over L_\text{rozpr}} \tag{5}$$

dla danego typu transformatora TrN. Iloraz ten mówi nam ile razy indukcyjność pierwotna tego transformatora jest większa od indukcyjności rozproszenia przeniesionej na uzwojenie pierwotne. W moich pobieżnych pomiarach:

• $k=100$ dla transformatora sieciowego typu E,
• $k=500$ dla transformatora sieciowego toroidalnego.
• W transformatorach audio współczynnik $k$ jest rzędu co najmniej kilku tysięcy.

2. Obliczenie wstępne indukcyjności pierwotnej TrN

$$L_\text{pierw wst} = kL_\text{rozpr wst} \tag{6}$$

gdzie $\boldsymbol{L_\textbf{rozpr wst}=50\textbf{ mH}}$. Podana wartość $L_\text{rozpr wst}$ odnosi się do warunków rys. 3 i jest proporcjonalna do przyjętej $R$.

3. Wyliczenie wstępnej dolnej częstotliwości granicznej transformatora APTS2 (przy spadku 3 dB)

$$f_\text{d wst} = {R \over 2\pi L_\text{pierw wst}} \tag{7}$$

gdzie $R$ jest rezystancją charakterystyczną APTS.

Ta wstępna wartość odnosi się do sytuacji przed przeskalowaniem względem przyjętej $f_\text{s}$.

4. Arbitralne wyznaczenie docelowego geometrycznego środka pasma $f_\text{s}$ transformatora APTS2 (1 kHz, jeśli korzystamy z wniosków rysunku 3).

5. Oszacowanie wstępnej górnej częstotliwości granicznej $f_\text{g wst}$ (−3 dB) transformatora APTS2 przy założeniu, że TrW pracuje od $\boldsymbol{2f_\textbf{s}=2f_\textbf{p wst}=2\textbf{ kHz}}$. Powyżej przyjmowałem przeciętne pasmo transformatora TrW, pozwalające sięgnąć $f_\text{g wst}=200\text{ kHz}$. Oszacowanie to opiera się na przeświadczeniu o minimalnych możliwościach naszego TrW.

6. Wyliczenie docelowych charakterystycznych częstotliwości transformatora APTS2 (przeskalowanie względem przyjętej $f_\text{s}$ wartości wstępnych):

$$f_\text{d} = {f_\text{s} \over \sqrt{f_\text{g wst} \over f_\text{d wst}}} \tag{8}$$

$$f_\text{g} = f_\text{s} \sqrt{f_\text{g wst} \over f_\text{d wst}} \tag{9}$$

$$f_\text{p} = f_\text{p wst} {f_\text{g} \over f_\text{g wst}} \tag{10}$$

Dalsze obliczenia będą się opierać już na przeskalowanych wartościach.

7. Obliczenie indukcyjności uzwojenia pierwotnego TrN wg. wzoru

$$L_\text{pierw} = {R \over 2\pi f_\text{d}} \tag{11}$$

Oczywiście należy mieć na uwadze konieczność przenoszenia przez TrN pasma do $f_\text{p}$. Gdyby tak nie było, co jest mało prawdopodobne, należy zmniejszyć indukcyjność wyliczoną w p.2 i powtórzyć obliczenia.

8. Obliczenie $L$ i $C$ wg. (1) i (2). Przypominam, że $L$ jest indukcyjnością uzwojenia pierwotnego TrW.

9. Rozłożenie pojemności $C$ na $C_1$ i $C_2$ wg. (3) i (4).

Już w tym miejscu należy oszacować, czy wskutek zastosowania TrN o bardzo dużym $k$ pojemność jego uzwojenia pierwotnego nie przekroczy $C_1$. Jeśli przekroczy (co jest mało prawdopodobne), należy zmniejszyć indukcyjność wyliczoną w p.2 i powtórzyć obliczenia.

10. Obliczenie uzwojeń wtórnych składowych transformatorów z zachowaniem równości obu przekładni.

Przykład

Poniżej obliczę transformator APTS2 wg. praktycznej procedury projektowej. Pogrubione zostały parametry końcowe.

1. Przyjmuję $\boldsymbol{k = 500}$.

2. Wg. (6): $L_\text{pierw wst} = 25\text{ H}$.

3. Przyjmując $\boldsymbol{R = 5\textbf{ kΩ}}$ (w p.2 przyjąłem $L_\text{rozpr wst} = 50\text{ mH}$), wg. (7): $f_\text{d wst} = 31.8\text{ Hz}$.

4. Obieram $\boldsymbol{f_\textbf{s} = 1\textbf{ kHz}}$ (korzystam z wniosków rys. 3).

5. Przewiduję, że wykonany przeze mnie TrW osiągnąłby wstępną $f_\text{g wst} = 200\text{ kHz}$.

6. Docelowe charakterystyczne częstotliwości transformatora APTS2 przedstawiają się następująco:

• Wg. (8): $\boldsymbol{f_\textbf{d} = 12.6\textbf{ Hz}}$.
• Wg. (9): $\boldsymbol{f_\textbf{g} = 79.3\textbf{ kHz}}$.
• Wg. (10): $\boldsymbol{f_\textbf{p} = 397\textbf{ Hz}}$.

Osiągnięte pasmo wydaje się zachęcać do eksperymentów nad transformatorami APTS2 :-)

7. Indukcyjność uzwojenia pierwotnego TrN wg. (11) wynosi: $\boldsymbol{L_\textbf{pierw}=63.2\textbf{ H}}$. Od razu otrzymujemy też $\boldsymbol{L_\textbf{rozpr}=126\textbf{ mH}}$.

8. Wartości $L$ i $C$:

• Indukcyjność uzwojenia pierwotnego TrW wg. (1) wynosi: $\boldsymbol{L = 1\textbf{ H}}$.
• Pojemność "widziana" na zaciskach uzwojenia pierwotnego TrN wg. (2) wynosi: $\boldsymbol{C = 160\textbf{ nF}}$.

9. Rozdział pojemności $C$ wygląda następująco:

• Wg. (3): $\boldsymbol{C_1 = 80\textbf{ nF}}$.
• Przyjmując $\boldsymbol{R_\textbf{o}=8\textbf{ Ω}}$ wg. (4): $\boldsymbol{C_2=50\textbf{ µF}}$.

Łatwo zauważyć, że $C_1$ praktycznie nie zależy od tolerancji pojemności uzwojenia pierwotnego TrN (oczywiście podobnie $C_2$).

10. Obliczenie parametrów uzwojeń wtórnych pomijam.

Na rys. 12 i 13 przedstawiam wyniki symulacji obliczonego wyżej transformatora APTS2. Ze względu na skończoną wartość $R_\text{g}$ (trioda / pentoda + USZ z anody), pasmo pokazane na tych rysunkach jest szersze od wyliczonego powyżej.

Podsumowanie

Omówiony APTS2 może być wstępem do realizacji APTS3 i więcej, przenoszących jeszcze szersze pasmo częstotliwości (rys. 14 i 15). Takie APTS są filtrami APF już wyższego rzędu, ale z wzajemnie rozsuniętymi częstotliwościami podziału $f_\text{p}$ (tak jakby wiele różnych APF1).

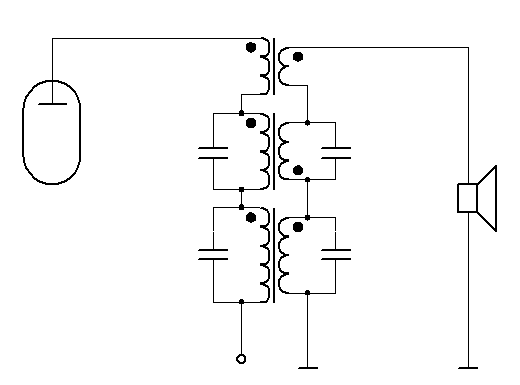
Przyjmując na rysunkach 14 i 15 dla każdego składowego transformatora $f_\text{g}/f_\text{d}$ równe średnio 50, pasmo takiego APTS3 można oszacować na 2.8 Hz – 350 kHz !!!

Zachęcam do eksperymentów z transformatorami APTS mającymi na celu rezygnację z wykonywania jednego kosztownego szerokopasmowego transformatora.

Historia artykułu
2001-02-23: powstanie
2014: korekta po przejściu na Joomla (ostatni stat. HTML)
2023-12-07: dopiski i korekta po przejściu z J3 na J5
2025-02-20: wprowadzenie nazwy APTS, nowy format wyrażeń/wzorów i korekta

© Copyright Krzysztof Kolisz 2001-02-23