Analiza teoretyczna
Zbudujmy model APTS składający się z dwóch transformatorów, czyli APTS2 (rys. A2).

Warunkiem wstępnym jest równość przekładni obu transformatorów. W celu wyeliminowania zjawisk nie będących przedmiotem analizy, dokonajmy następujących uproszczeń:
- Przekładnie obu składowych transformatorów $n_\text{n}=n_\text{w}=n=1$, gdzie $n=z_2/z_1$ i $z_1$ – liczba zwojów uzwojenia pierwotnego, a $z_2$ – wtórnego. Oczywiście w ogólnym przypadku $n^2=R_\text{o}/R_\text{g}$.
- Współczynniki sprzężenia pomiędzy uzwojeniami pierwotnym i wtórnym obu transformatorów są równe $1$.
- Pojemności wejściowa i wyjściowa transformatora niskotonowego TrN są skupione na jego uzwojeniu pierwotnym.
- W dalszej części wyeliminujemy dolne ograniczenie pasma przenoszenia układu.
Transmitancja napięciowa modelu APTS2 (rys. A2) opisana jako wzmocnienie transmisyjne napięć przedstawia się następująco
$$T_1(s) = {u_\text{wy}(s) \over e_\text{g}(s)} = {-R_\text{o}L_\text{n}L_\text{w}Cs^3+R_\text{o}(L_\text{n}-L_\text{w})s \over (R_\text{g}+R_\text{o})L_\text{n}L_\text{w}Cs^3+(R_\text{g}R_\text{o}C+4L_\text{w})L_\text{n}s^2+(R_\text{g}+R_\text{o})(L_\text{n}+L_\text{w})s+R_\text{g}R_\text{o}}\tag{B1}$$
gdzie $s=\mathrm{j}\omega$ jest zmienną zespoloną, tutaj ograniczoną do osi urojonej (widma).
W celu eliminacji ograniczenia pasma przenoszenia od strony najniższych częstotliwości, zostanie znacznie zwiększona wartość indukcyjności $L_\text{n}$
$$T_2(s) = \lim_{L_\text{n} \to \infty}T_1(s) = {-R_\text{o}L_\text{w}Cs^2+R_\text{o} \over (R_\text{g}+R_\text{o})L_\text{w}Cs^2+(R_\text{g}R_\text{o}C+4L_\text{w})s+R_\text{g}+R_\text{o}}\tag{B2}$$
W ten sposób wpływ tej indukcyjności został w dalszej analizie zlikwidowany tzn. nasz model przenosi teraz nawet składową stałą. Zauważmy, że dla $\omega=0$ transmitancja (B2) wynosi ${R_\text{o} \over R_\text{g}+R_\text{o}}$ (patrz wyrazy wolne w liczniku i mianowniku), natomiast dla $\omega\to\infty$ transmitancja ta zmierza do ${-R_\text{o} \over R_\text{g}+R_\text{o}}$ (przeciwfaza, patrz współczynniki przy $s^2$). Mamy więc potwierdzenie, że APTS2 jest filtrem APF1, co wynika z odwróconego połączenia uzwojeń wtórnych transformatorów składowych.
Teraz interesować nas będzie uzyskanie w modelu APTS2 stałości jedynie modułu $|T_2(\omega)|$ (niezależnie od $\omega$), gdyż z faktu, że jest on filtrem APF1 wynika niemożność uzyskania stałości fazy.
$$|T_2(\omega)| = {R_\text{o}L_\text{w}C\omega^2+R_\text{o} \over \sqrt{(R_\text{g}+R_\text{o})^2L_\text{w}^2C^2\omega^4+[R_\text{g}^2R_\text{o}^2C^2-2(R_\text{g}-R_\text{o})^2L_\text{w}C+16L_\text{w}^2]\omega^2+(R_\text{g}+R_\text{o})^2}}\tag{B3}$$
Do przeanalizowania przebiegu $|T_2(\omega)|$ potrzebna nam będzie pochodna tej funkcji względem pulsacji $\omega$
$${\mathrm{d}|T_2(\omega)| \over \mathrm{d}\omega} = {R_\text{o}(R_\text{g}^2C-4L_\text{w})(R_\text{o}^2C-4L_\text{w})(L_\text{w}C\omega^2-1)\omega \over \lbrace\sqrt{(R_\text{g}+R_\text{o})^2L_\text{w}^2C^2\omega^4+[R_\text{g}^2R_\text{o}^2C^2-2(R_\text{g}-R_\text{o})^2L_\text{w}C+16L_\text{w}^2]\omega^2+(R_\text{g}+R_\text{o})^2}\rbrace^3}\tag{B4}$$
Warunkiem uzyskania stałości funkcji $|T_2(\omega)|$ jest występująca dla każdej wartości $\omega$ równość
$${\mathrm{d}|T_2(\omega)| \over \mathrm{d}\omega} = 0 \tag{B5}$$
Ogólnym, mającym fizyczny sens rozwiązaniem równania (B5) jest spełnienie przynajmniej jednej z trzech poniższych równości
$$C = {4L_\text{w} \over R_\text{g}^2} \tag{B6}$$
$$C = {4L_\text{w} \over R_\text{o}^2} \tag{B7}$$
$$\omega^2 = {1 \over L_\text{w}C} \tag{B8}$$
Wyrażenia (B6) i (B7) są interesującymi nas rozwiązaniami, gdyż nie zależą od $\omega$. Na ich podstawie definiujemy rezystancję charakterystyczną $\boldsymbol{R}$ transformatora APTS (rys. A2)
$$\boxed{R \stackrel{\text{def}}{=} 2\sqrt{L_\text{w} \over C}} \tag{B9}$$
Rozwiązanie (B8) informuje nas o istnieniu jednego ekstremum funkcji $|T_2(\omega)|$, które oczywiście zanika przy spełnieniu równania (B6) lub (B7). Występuje ono na pulsacji rezonansowej szeregowego obwodu rezonansowego $L_\text{w}C$. Nazwijmy pulsację występowania tego w zasadzie potencjalnego ekstremum pulsacją podziału $\boldsymbol{\omega_\textbf{p}}$ transformatora APTS, jako że występuje w tym punkcie równomierny podział napięcia pomiędzy oboma transformatorami składowymi
$$\boxed{\omega_\text{p} = {1 \over \sqrt{L_\text{w}C}}} \tag{B10}$$
Ostatecznie na podstawie (B9) i (B10) otrzymujemy wzory projektowe transformatora APTS
$$\boxed{L_\text{w} = {R \over 2\omega_\text{p}}} \tag{B11}$$
$$\boxed{C = {2 \over \omega_\text{p}R}} \tag{B12}$$
Z (B6), (B7) i (B9) wynika warunek stałości $|T_2(\omega)|$. Wystarczy spełnić jedną z następujących dwóch równości lub inaczej – warunków dopasowania
$$\boxed{R_\text{g} = R} \tag{B13}$$
$$\boxed{R_\text{o} = R} \tag{B14}$$
Wtedy to niezależnie od $\omega$ moduł transmitancji APTS2 będzie równy (rys. A3 i A4)
$$|T_2(\omega)| = {R_\text{o} \over R_\text{g}+R_\text{o}} = \mathrm{const} \tag{B15}$$

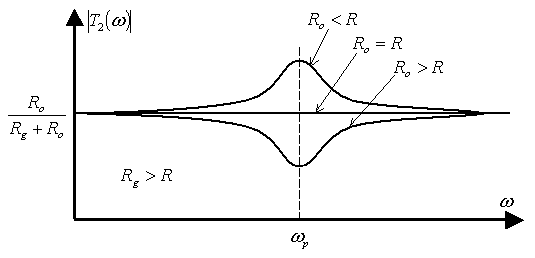
Analiza przebiegu modułu impedancji wejściowej $|Z_\text{we}(\omega)|$ "widzianej" na prawo od $R_\text{g}$ (rys. A2 i A5) pokazuje, że jest ona niezależna od $\omega$ jedynie przy $R_\text{o}=R$. Impedancja ta ma wtedy charakter rezystancji i jest równa $R$. Przy dowolnych wartościach $R_\text{o}$ impedancja wejściowa $Z_\text{we}(\omega_\text{p})$ transformatora APTS2 przypomina impedancję wejściową ćwierćfalowej linii długiej – jest odwrotnością $R_\text{o}$ względem $R$ zawsze mając charakter rezystancyjny.

Ostatecznie, ze względu na możliwość wahań rezystancji $R_\text{o}$, korzystnie jest przyjąć mocniejszą zasadę
$$R_\text{g} = R = R_\text{o} \tag{B16}$$
To niezwykłe zachowanie się APTS2 na rys. A4 i A5 przy $\omega=\omega_\text{p}$ można wytłumaczyć transformacyjnymi właściwościami szeregowego obwodu rezonansowego $L_\text{w}C$. W szczególności przebieg $|Z_\text{we}(\omega)|$ (im mniejsza $R_\text{o}$ tym większy $|Z_\text{we}(\omega_\text{p})|$) można wyjaśnić następująco: niska rezystancja $R_\text{o}$ przytłumia szeregowy obwód rezonansowy $L_\text{w}C$, nie pozwalając mu na osiągnięcie "w pełni" rezonansu (dużej dobroci $Q$), a tym samym zera omów na jego wejściu.
Analizując wpływ dokonanych na wstępie uproszczeń, w celu powrotu do praktycznego schematu APTS2 z rys. 1 trzeba wymienić:
- Przyjmując przekładnie transformatorów $n_\text{n}=n_\text{w}=n\neq 1$, zamiast $R_\text{o}$ we wzorach trzeba wstawić $R_\text{o}'={R_\text{o}\over n^2}$ ($R_\text{o}$ przeniesione na wejście). Stosownie do przekładni $n$ ulegają zmianie indukcyjności uzwojeń wtórnych obu transformatorów składowych. Dodatkowo, jeśli naruszymy warunek $n_\text{n}=n_\text{w}$, zostanie zdeformowana charakterystyka przenoszenia APTS2.
- Rozkładając pojemność $C$ na dwie $C_1$ i $C_2$ wydaje się najkorzystniejszym dokonać równego podziału na jednakowe reaktancje względne po obu stronach TrN tzn. $C_1={C\over2}$, $C_2={C\over2n^2}$. To zalecenie ma jednak naturę tylko praktyczną.
- Przyjmując skończoną wartość $L_\text{n}$, trzeba zapewnić pojemność zastępczą równoległego obwodu rezonansowego $L_\text{n}C_\text{n}$ (gdzie $C_\text{n}$ są pojemnościami „wlutowanymi” oraz uzwojeń, przeniesionymi na wejście TrN) przy $\omega_\text{p}$ zbliżoną do $C$. Jednak w praktyce wpływ ten jest względnie mały.