Impedancja wejściowa linii długiej

Przedstawiam nową odsłonę mojego artykułu sprzed 18 lat o impedancji wejściowej linii długiej. Temat zjawisk zachodzących w fiderze nigdy się nie starzeje. W obecnej wersji artykułu uwzględniłem fazę, odnowiłem rysunek i wykresy, dodałem wykresy 3D i animację, przeformatowałem wzory i przeredagowałem cały tekst. Zapraszam do lektury :-)

Omówimy zjawiska zachodzące w fiderze mogące zainteresować krótkofalowca – praktyka. Nie będziemy więc analizować napięć i prądów wzdłuż linii długiej, ale skupimy się na jej impedancji wejściowej. Ma to bezpośredni wpływ na pracę nadajnika.

Przeanalizujemy impedancję wejściową $Z_\text{we}$ linii długiej o impedancji falowej $Z_0$ w zależności od impedancji końcowej $Z_\text{k}$ (obciążenia np. anteny) oraz długości linii $x$ (rys. 1).

Rysunek 1 można interpretować dwojako:

1. Oznaczenie $x$ to długość fidera. Dobierając $x$ np. skracając kabel, w pewnych warunkach możemy zmieniać $Z_\text{we}$ całego schematu z rys. 1. Podejście to umożliwi nam poznanie wpływu długości fidera na impedancję widzianą przez nadajnik.
2. Oznaczenie $x$ to punkt fidera o nieistotnej dla nas długości większej od $x$. Takie podejście pozwoli przeanalizować stosunek napięcia do prądu w dowolnym punkcie $x$ linii długiej. Dzięki temu poznamy interesujące właściwości fali stojącej, występujące również w promiennikach anten, ale też szerzej np. w akustyce.

Wyrażenie określające impedancję wejściową $\boldsymbol{Z_\textbf{we}}$ układu z rysunku 1 przedstawia się następująco [1]

$$\boxed{Z_\text{we}(x) = Z_0 {{Z_\text{k}+Z_0\tanh(\gamma x)} \over {Z_\text{0}+Z_\text{k}\tanh(\gamma x)}}} \tag{1}$$

gdzie $x$ jest odległością w metrach badanych zacisków wejściowych od końca linii, a

$$Z_0 = \sqrt{{R+\mathrm{j}\omega L} \over {G+\mathrm{j}\omega C}} \quad \gamma = \sqrt{(R+\mathrm{j}\omega L)(G+\mathrm{j}\omega C)} \tag{2}$$

impedancją falową $\boldsymbol{Z_0}$ linii oraz jej stałą propagacji $\boldsymbol{\gamma}$ (małe gamma). Nie będziemy się dalej zajmować stałą propagacji.

Jak widać, linię długą można przedstawić przy pomocy czterech parametrów rozłożonych:

$R\text{ [Ω/m]}$ – rezystancja jednostkowa razem obu przewodów linii np. środkowej żyły i ekranu kabla koncentrycznego,
$G\text{ [S/m]}$ (simens/metr) – konduktancja jednostkowa pomiędzy oboma przewodami linii (upływność izolacji) np. między środkową żyłą, a ekranem,
$L\text{ [H/m]}$ – indukcyjność jednostkowa razem obu przewodów linii np. środkowej żyły i ekranu,
$C\text{ [F/m]}$ – pojemność jednostkowa między oboma przewodami linii np. między środkową żyłą, a ekranem.

W praktyce łatwo można wykonać pomiar $L$ i $C$ zwykłym multimetrem (niska $f$ pomiaru) podłączonym na wejście linii: przy pomiarze $L$ linię na końcu zwieramy, natomiast przy pomiarze $C$ rozwieramy. Następnie oba wyniki dzielimy przez długość tak zmierzonego odcinka linii $x$ w metrach.

Zapoznajmy się jeszcze z wzorami na współczynnik odbicia $\boldsymbol{\mathit{\Gamma}}$ (duże gamma) i współczynnik fali stojącej $\boldsymbol{\mathit{SW\!R}}$:

$$\mathit{\Gamma} = {{Z_\text{k}-Z_0} \over {Z_\text{k}+Z_0}} \quad \boxed{\mathit{SWR} = {{1+|\mathit{\Gamma}|} \over {1-|\mathit{\Gamma}|}}} \tag{3}$$

Na rysunkach 1a i 1b możemy "zobaczyć" wzory (3). Wynika z nich między innymi, że każda odchyłka $X_\text{k}$ od zerowej wartości jest z punktu widzenia $\mathit{SWR}$ nie do "odratowania" tzn. nie można już jej zniwelować doborem $R_\text{k}$.

Spokojnie, nie będziemy dowodzić i jakoś specjalnie analizować powyższych wzorów, z pomocą przyjdą nam opierające się na wzorze (1) wykresy. Jednak nie będą to dedykowane do tego celu wykresy Smitha, ale pozostaniemy przy prostokątnym układzie współrzędnych, naturalniejszym dla obserwacji najprostszych zależności.

A zatem jak ma się wzór (1) do praktyki krótkofalarskiej?

Przede wszystkim zauważmy, że przy $\boldsymbol{Z_\textbf{k} = Z_0}$ np. dopasowaniu anteny do fidera, wyrażenie (1) przekształca się do postaci

$$\boxed{Z_\text{we}(x) = Z_0} \tag{4}$$

Wówczas impedancja wejściowa $\boldsymbol{Z_\textbf{we}(x)}$ układu z rys. 1 nie zależy od długości $\boldsymbol{x}$ fidera, czy jego tłumienia i jest równa $\boldsymbol{Z_0}$. Ponadto zgodnie z (3) zachodzi: $\mathit{\Gamma} = 0$ i $\mathit{SWR} = 1$, czyli w fiderze nie występuje fala stojąca.

Jeśli Twoja antena spełnia $Z_\text{k} = Z_0$, omawiane dalej tematy mogą nie być dla Ciebie interesujące :-( Obawiam się jednak, że w sensownym zakresie częstotliwości mało która instalacja antenowa to spełnia, więc zachęcam do kontynuacji niniejszej lektury :-)

Na wstępie krótka przypominajka liczb zespolonych.

Liczby zespolone

Liczbę zespoloną $z = a + \mathrm{j}b$ reprezentuje para liczb: część rzeczywista $a$ i część urojona $\mathrm{j}b$. Symbol $\boldsymbol{\mathrm{j}}$ (w matematyce stosuje się oznaczenie $\boldsymbol{\mathrm{i}}$) to jednostka urojona, która ma taką własność, że $\mathrm{j}^2 = −1$, co jest niemożliwe do realizacji na liczbach rzeczywistych, gdyż kwadrat każdej liczby rzeczywistej jest nieujemny.

W przypadku omawianej w niniejszym artykule impedancji $Z$, reprezentowana jest ona przez zapis $Z = R + \mathrm{j}X$ czyli parę: rezystancję $R$ i reaktancję $X$. Liczbę zespoloną, w tym również impedancję, można też wyrazić inną parą: modułem $|Z|$ i argumentem (fazą) $\mathit{\Phi}$, gdzie

$$|Z| = \sqrt{R^2+X^2}, \quad \tan\mathit{\Phi} = {{X} \over {R}}$$

Każde z tych podejść (par) jednoznacznie identyfikuje liczbę zespoloną np. impedancję.

W elektrotechnice potocznie mówi się, że impedancja $Z$ ma charakter rzeczywisty lub rezystancyjny, gdy $X = 0\text{ Ω}$, cechę taką posiada rezystor, którego impedancja $Z = R$. Podobnie mówi się, że impedancja $Z$ ma charakter urojony lub reaktancyjny, gdy $R = 0\text{ Ω}$ i $X \neq 0\text{ Ω}$ – wówczas jeśli $X > 0\text{ Ω}$, to reaktancja ta jest indukcyjna ($Z = \mathrm{j}X_\text{L}$), a gdy $X < 0\text{ Ω}$, reaktancja jest pojemnościowa ($Z = \mathrm{j}X_\text{C}$).

W przypadku admitancji $Y = 1/Z = G + \mathrm{j}B$, gdzie $B$ jest susceptancją pojemnościową lub indukcyjną. Dla danego elementu obwodu jest $G = 1/R$ i $B = 1/X$, a znak $B$ jest przeciwny do znaku $X$.

Przykładowo, weźmy wzory (2). Występuje w nich impedancja $Z = R + \mathrm{j}\omega L$, gdzie reaktancja indukcyjna $X_\text{L} = \omega L$. Jest tam też admitancja $Y = G + \mathrm{j}\omega C$, gdzie susceptancja pojemnościowa $B_\text{C} = \omega C$.

Reprezentatywnym przykładem jest szeregowy obwód rezonansowy RLC, którego impedancja $Z = R + \mathrm{j}X_\text{L} + \mathrm{j}X_\text{C} = R + \mathrm{j}\omega L − \mathrm{j}{1 \over {\omega C}}$. Podobną naturę ma impedancja wejściowa anteny dipol symetryczny. W rezonansie takiego obwodu zachodzi $X = X_\text{L} + X_\text{C} = 0$ (kompensacja obu reaktancji) i wówczas $Z = R$. Oznacza to, że dla częstotliwości rezonansowej (pulsacji $\omega_0$) na swych zaciskach reprezentuje on rezystancję $R$ (zachowuje się jak zwykły rezystor).

Powróćmy do tematu linii długiej.

Linia bezstratna

W dalszych rozważaniach załóżmy częstotliwość sygnału $30\text{ MHz}$. Została ona dobrana dość wysoko jak na pasmo KF, ale dzięki temu urealnimy omówioną dalej tłumienność kabla. Teraz przyjmijmy fider o parametrach:

$$L = \boldsymbol{250}\text{ nH/m}, \,\, C = \boldsymbol{100}\text{ pF/m}, \,\, R = \boldsymbol{0}\text{ Ω/m}, \,\, G = \boldsymbol{0}\text{ S/m}$$

Mamy więc kabel bezstratny ($R = 0$ i $G = 0$) o typowych wartościach $L$ i $C$ oraz impedancji falowej $Z_0 = R_0 + \mathrm{j}X_0 = R_0 = 50\text{ Ω}$, a więc o charakterze rezystancyjnym (rzeczywistym) tzn. jego reaktancja falowa $X_0 = 0$ (składowa urojona). Charakter ten wynika ze skrócenia się jednostki urojonej $\mathrm{j}$ we wzorze (2) na $Z_0$ mające miejsce przy zerowych $R$ i $G$. W całym artykule przyjmujemy $\boldsymbol{Z_0 = R_0}$, a teoretyczne odstępstwa od tego założenia omówimy dalej.

Po obciążeniu takiej linii długiej impedancją $Z_\text{k} = R_\text{k} + \mathrm{j}X_\text{k} = R_\text{k}$, czyli również o charakterze rezystancyjnym ($X_\text{k} = 0$), równą jej impedancji falowej tzn. $Z_\text{k} = Z_0 = 50 + \mathrm{j}0\text{ Ω} = 50\text{ Ω}$, mamy dopasowanie obciążenia do linii długiej otrzymując przebieg $Z_\text{we}(x)$ pokazany na rys. 2.

Zgodnie z wcześniejszym spostrzeżeniem (4) otrzymaliśmy impedancję wejściową $Z_\text{we}(x) = Z_0$ niezależnie od długości $x$ przewodu. Jest to sytuacja identyczna z tą, gdybyśmy podłączyli $Z_\text{k}$ bezpośrednio na wyjście nadajnika (bez udziału fidera), nawet przy zmianach częstotliwości.

Naruszmy teraz warunek dopasowania $Z_\text{k} = Z_0$, niech będzie $Z_\text{k} = 100\text{ Ω}$, czyli $Z_\text{k}$ jest $2$ razy większa od $Z_0$ (rys. 3).

No i tu zaczynają się "schody" (czytaj: możliwość zaobserwowania wiele ciekawych zjawisk :-)

Najpierw rozpatrzmy interpretację opierającą się na zmiennej długości $x$ fidera.

Przy zerowej długości ($x = 0$, brak fidera) otrzymujemy łatwą do przewidzenia wartość $Z_\text{we}(0) = Z_\text{k} = 100\text{ Ω}$, co oczywiście daje $\mathit{\Phi}_\text{we}(0) = 0^\circ$. Przy zwiększaniu $x$ zmniejsza się moduł impedancji $|Z_\text{we}(x)|$ zbliżając się przy $x = 0.83\text{ m}$ do $|Z_0| = 50\text{ Ω}$, choć wówczas faza nie jest już zerowa i wynosi $\mathit{\Phi}_\text{we}(0.83) = −37^\circ$. Przy dalszym zwiększaniu długości kabla $x$ dochodzimy do $|Z_\text{we}(\lambda/4)| = 25\text{ Ω}$, gdzie $\lambda$ jest długością fali w naszej linii długiej, znowu z zerową fazą itd. w dalszym etapie otrzymując oscylacyjne zmiany $|Z_\text{we}(x)|$ co pół długości fali $\lambda$. Na podstawie tych wykresów możemy wyznaczyć $\boldsymbol{\lambda \approx 6.7\textbf{ m}}$ oraz współczynnik skrócenia $\boldsymbol{0.67}$ (długość fali w próżni przy $30\text{ MHz}$ wynosi około $10$ metrów).

Zasadniczym spostrzeżeniem są granice zmian przebiegu $|\boldsymbol{Z_\textbf{we}(x)|}$  – wg. rysunku 3 są to wspomniane wartości $Z_\text{we min} = R_\text{we min} = 25\text{ Ω}$ i $Z_\text{we max} = R_\text{we max} = 100\text{ Ω}$. A więc w tym przypadku zachodzi

$$\boxed{\mathit{SWR} = \sqrt{{R_\text{we max}} \over {R_\text{we min}}} = \sqrt{{Z_\text{we max}} \over {Z_\text{we min}}} = \left. {{Z_\text{we max}} \over {Z_0}} \right|_{Z_0=R_0} = \left. {{Z_0} \over {Z_\text{we min}}} \right|_{Z_0=R_0}} \tag{5}$$

Na rys. 3 współczynnik fali stojącej $\mathit{SWR}$ jest niezależny od długości $x$ fidera (wykresy na lewo od $x$ nie ulegają zmianie) i wynosi $\mathit{SWR} = 2$. Wynika to też ze wzorów (3) na $\mathit{\Gamma}$ i $\mathit{SWR}$, które dla linii bezstratnej nie zależą od $x$, a jedynie od $Z_0$ i $Z_\text{k}$. Okazuje się, że po podstawieniu w nich $Z_\text{k} = Z_\text{we}(x)$, wyliczony z tych wzorów $\mathit{SWR}$ wciąż będzie niezależny od $x$. Na wykresie Smitha jest to tzw. okrąg stałego $|\mathit{\Gamma}|$. Oznacza to, że zasadniczo miernik fali stojącej (reflektometr) powinien wskazywać poprawny $\mathit{SWR}$ niezależnie od miejsca jego załączenia np. przy antenie lub przy nadajniku. W praktyce jednak wskazania reflektometru mogą nieco zależeć od $x$ w wyniku istnienia składowej współbieżnej fali fidera np. w asymetrycznej antenie FD4.

Zatrzymajmy się na chwilę na praktycznych dla krótkofalowca aspektach fali stojącej.

Zasadniczo istnienie fali stojącej w fiderze nie musi być zjawiskiem negatywnym. Niektóre anteny np. G5RV i Doublet, projektowo mają taką falę stojącą w części lub w całym fiderze w celu dopasowania do anteny. Do niekorzystnych skutków istnienia fali stojącej w fiderze można zaliczyć nieco większe straty w linii (głównie na wyższych częstotliwościach), które zmniejsza się stosowaniem możliwie bezstratnych fiderów np. kabli koncentrycznych o dużej średnicy, symetrycznych drabinek. Ponadto fala stojąca może być powodem promieniowania elektromagnetycznego fidera, które może objawiać się jako zakłócenia TVI. Tutaj linie symetryczne dobrze tłumią takie promieniowanie.

Załóżmy sytuację istnienia fali stojącej w fiderze tzn. $\mathit{SWR} > 1$. Objawia się to zmianami $Z_\text{we}(x)$ wraz ze zmianą $x$. Jeśli dla ustalonego $x$ dopasujemy $Z_\text{we}(x)$ do optymalnej rezystancji obciążenia nadajnika $R_\text{nad}$ za pomocą idealnej skrzynki antenowej, cała rzeczywista moc wyjściowa nadajnika np. $100\text{ W}$, zostanie przekazana do fidera. Jeśli fider będzie bezstratny (można tak przyjąć na niższych pasmach KF), cała ta moc zostanie wypromieniowana w eter, choć niestety w części może odbyć się to przez fider jak np. w przypadku anteny FD4. Jeśli jednak fider nie będzie promieniował (symetryczna drabinka w antenie Doublet), cała moc nadajnika przejdzie do $R_\text{k}$ mimo iż może być $X_\text{k} \neq 0$. Wynika to z prawa zachowania energii zrealizowanego dopasowaniem przez fider. Wówczas dla idealnej anteny moc wypromieniowana będzie równa całe $100\text{ W}$.

Powracając do rys. 3 zauważmy, że $Z_\text{we}(x)$ ma charakter rezystancyjny jedynie przy długości fidera równej wielokrotności $\lambda/4$ tzn. dla $x = x_n = n\lambda/4$, gdzie $n = 0,\,1,\,2,\,\ldots\,$ jest liczbą naturalną. Jedynie wówczas reaktancja $X_\text{we}(x_n) = 0\text{ Ω}$ (wykres czerwony), więc też faza $\mathit{\Phi}_\text{we}(x_n) = 0^\circ$ (zielony), a nadajnik obciążony jest rezystancją (niebieski) o jednej z dwóch wspomnianych granicznych wartościach $25$ lub $100\text{ Ω}$. Niestety, nie ma wśród nich wartości $Z_0 = 50\text{ Ω}$ :-(

Bardzo ważną własnością linii długiej jest fakt, że przy parzystych $n$ tzn. przy wielokrotnościach $\lambda/2$, zachodzi $Z_\text{we}(x_{2n}) = Z_\text{k}$. Oznacza to, że z punktu widzenia nadajnika dla takiej wynikającej z tego siatki częstotliwości fider jest "przezroczysty" tak, jakbyśmy podłączyli $Z_\text{k}$ wprost do nadajnika. Jednak fizycznie fider nadal istnieje mając falę stojącą (na rys. 3 jest niezmiennie $\mathit{SWR} = 2$), która może generować promieniowanie elektromagnetyczne powodując zakłócenia TVI.

I tu na chwilę przejdźmy do interpretacji rys. 1 opierającej się na obserwacji fali stojącej w punkcie $x$ fidera mającego długość większą od $x$ np. na rys. 3 może to być fider o nieistotnej dla nas długości przekraczającej zakres tego rysunku np. $15$ metrów.

Z rys. 3 wynika, że fala stojąca obciąża swoje źródło zasilania w sposób rezystancyjny jedynie w swych strzałkach i węzłach tzn. w punktach $\boldsymbol{x = x_n}$. Natomiast dla $x \neq x_n$ fala stojąca obciąża swe źródło zasilania również niezerową reaktancją $X_\text{we}$. Ważnym spostrzeżeniem jest fakt, że w obszarze $\boldsymbol{x \neq x_n}$ przesunięcie fazy między napięciem $\boldsymbol{u(x)}$, a prądem $\boldsymbol{i(x)}$ fidera wyrażone fazą $\boldsymbol{\mathit{\Phi}_\textbf{we}(x)}$ zawiera się w przedziale od $\boldsymbol{−90^\circ}$ do $\boldsymbol{+90^\circ}$. Jest to o tyle istotne, że jednocześnie jest to przedział możliwych wartości fazy $\mathit{\Phi}_\text{k}$, co umożliwia "dostosowanie" się przebiegów w linii do dowolnego jej obciążenia realizując fazowy warunek brzegowy linii długiej. Omówimy to szerzej na jednym z kolejnych wykresów.

Tak na marginesie, nie należy mylić fazy $\mathit{\Phi}_\text{we}(x)$ odnoszącej się do zadanego punktu $x$ linii długiej, z przesunięciem fazy między strzałkami napięcia, a strzałkami prądu tej linii. W tym drugim przypadku zawsze jest $\pm90^\circ$.

Nasuwa się pytanie, co z powyższych obserwacji wynika dla krótkofalowca?

Najważniejszym praktycznym wnioskiem jest fakt, że przy niedopasowaniu $\boldsymbol{Z_\textbf{k}}$ do $\boldsymbol{Z_0}$ (anteny do fidera) zmieniając długość $\boldsymbol{x}$ fidera możemy albo dopasować $\boldsymbol{|Z_\textbf{we}(x)|}$ do optymalnej rezystancji obciążenia nadajnika $\boldsymbol{R_\textbf{nad}}$ albo wyzerować fazę $\boldsymbol{\mathit{\Phi}_\textbf{we}(x)}$, ale nie obie te rzeczy jednocześnie. Najprostszym tego wyjaśnieniem jest fakt, że zmianą długości $x$ fidera (tylko jeden parametr) próbujemy dopasować aż dwa niezależne parametry tzn. moduł $|Z_\text{we}(x)|$ i fazę $\mathit{\Phi}_\text{we}(x)$. Inaczej jest np. w skrzynkach antenowych posiadających co najmniej dwie niezależne regulacje (przełącznik indukcyjności i pokrętło pojemności).

Jakie są tego praktyczne konsekwencje?

Nierówność $\boldsymbol{|Z_\textbf{we}(x)| \neq R_\textbf{nad}}$ nawet mimo $\boldsymbol{\mathit{\Phi}_\textbf{we}(x) = 0^\circ}$ jest przeciążeniem napięciowym lub prądowym nadajnika tzn. przekraczamy dopuszczalne napięcie lub prąd wyjściowy jego końcówki mocy, co w przypadku braku zabezpieczeń może doprowadzić do jego uszkodzenia.

Natomiast sytuacja $\boldsymbol{|Z_\textbf{we}(x)| = R_\textbf{nad}}$ oraz $\boldsymbol{\mathit{\Phi}_\textbf{we}(x) \neq 0^\circ}$ (na rys. 3 np. przy $x = 0.83\text{ m}$), stanowi tzw. trudne obciążenie zamieniające konstrukcyjną prostą pracy stopnia końcowego (lamp lub tranzystorów) na krzywą kształtem zbliżoną do elipsy (patrz krzywe Lissajous). Może to powodować pobór maksymalnego chwilowego prądu wyjściowego (na razie wszystko OK), ale w niewygodnych dla nadajnika chwilach okresu, kiedy to jego chwilowe napięcie wyjściowe jest dość niskie (czyli duże napięcia anodowe lub kolektora, sytuacja niezbyt OK). Może to zwiększyć moc strat (temperaturę) w lampach lub tranzystorach końcowych, a ponadto może to być ponad możliwości wzmocnienia prądowego stopni wzmacniacza, co doprowadzi do jego przesterowania. Termicznie sytuacja ta jest podobna do pracy liniowego zasilacza o regulowanym stałym napięciu wyjściowym, przy ustawieniu tego napięcia na dość niskim poziomie – wówczas tranzystory mocy tego zasilacza mogą być termicznie znacznie obciążane.

Nadajnik o znamionowej mocy np. $100\text{ W}$, może wtedy oddawać moc pozorną $S_\text{nad} = 100\text{ VA}$, ale moc czynna $P_\text{nad}$ będzie mniejsza od $100\text{ W}$, gdyż będzie niezerowa moc bierna $Q_\text{nad}$. Wynika to z ogólnej zależności: $S^2 = P^2 + Q^2$.

W szczególności nie zalecam załączania na wyjście nadajnika kondensatora mającego reaktancję $|X_\text{C}| = R_\text{nad}$. Jest to skrajnie trudne obciążenie, gdyż taki kondensator pobiera chwilowy prąd znamionowy przy chwilowym napięciu akurat przechodzącym przez wartość $0\text{ V}$. Wówczas też nadajnik oddaje tylko moc bierną, czyli dla typowego nadajnika $100\text{ W}$ jest $S_\text{nad} = Q_\text{nad} = 100\text{ VA}$ oraz moc czynna $P_\text{nad} = 0\text{ W}$.

Oczywiście, gdy jednocześnie jest $|Z_\text{we}(x)| \neq R_\text{nad}$ i $\mathit{\Phi}_\text{we}(x) \neq 0^\circ$, sytuacja jest najgorsza.

Jednak skrzynka antenowa łatwo radzi sobie z trudnym obciążeniem i przeciążeniem ukrywając ten problem przed nadajnikiem, choć może przekładać się to na podwyższone napięcia lub prądy w skrzynce. Jednak zmianą długości fidera możemy na poszczególnych pasmach obciążać skrzynkę bardziej przyjazną impedancją, co ułatwi jej zadanie. Wysoka wartość $\mathit{SWR} = 10$ może przykładowo oznaczać $|Z_\text{we}(x)| = 5$ lub $500\text{ Ω}$. Dla wielu skrzynek obciążenie $5\text{ Ω}$ jest poza ich zasięgiem (generalnie amatorskie skrzynki nie lubią niskich impedancji), natomiast większość skrzynek spokojnie poradzi sobie z $500\text{ Ω}$, co można osiągnąć właśnie stosowną długością fidera.

Nie będziemy rozstrzygać kwestii, czy zasilanie systemu antenowego w punktach $x_n$ jest korzystniejsze, co preferują zwolennicy posiadania fidera o długości równej wielokrotności $\lambda/4$, a najlepiej $\lambda/2$. Jednak jak wcześniej zauważyliśmy, dobór takiej długości fidera nie wpływa na wielkość jego fali stojącej (na rozkład napięć i prądów wzdłuż przewodu), a tym samym na jego $\boldsymbol{\mathit{SW\!R}}$. Również jak zauważyliśmy na wstępie artykułu, przy dopasowaniu $Z_\text{k} = Z_0$ długość fidera nie ma kompletnie żadnego znaczenia.

Z rys. 3 możemy też wywnioskować ciekawą analogię występującą na zaciskach wejściowych anten (bez fidera) w rezonansie. Uprawnia nas do tego fakt, że promieniujący przewód anteny np. LW, jest niejako również linią długą, ale rozwartą na końcu i posiadającą straty głównie promieniowania (nie $R$ i $G$ w sensie powyższym). Zatem analogia ta to: dipol i LW to rezystancja $R_\text{k}$, natomiast FD4 to trudne obciążenie z $X_\text{k} \neq 0\text{ Ω}$. Kwestię obciążenia linii długiej impedancją zespoloną (a dokładniej trudnym obciążeniem) omówimy dalej.

Również interesująca analogia jest w technice audio, gdzie niektóre kolumny głośnikowe reprezentujące takie trudne obciążenie powodują szybsze wpadanie wzmacniacza w zniekształcenia i przesterowanie (tu nie ma skrzynki antenowej ;-) Temat trudnego obciążenia jest jednym z podstawowych we wszelkich recenzjach kolumn głośnikowych. Ale bez obawy, nie będziemy tu analizować wpływu charakteru impedancji anteny na zawartość basów w SSB ;-)

Zobaczmy teraz co się stanie, jeśli zwiększymy $Z_\text{k}$ do wartości np. $500\text{ Ω}$ (rys. 4).

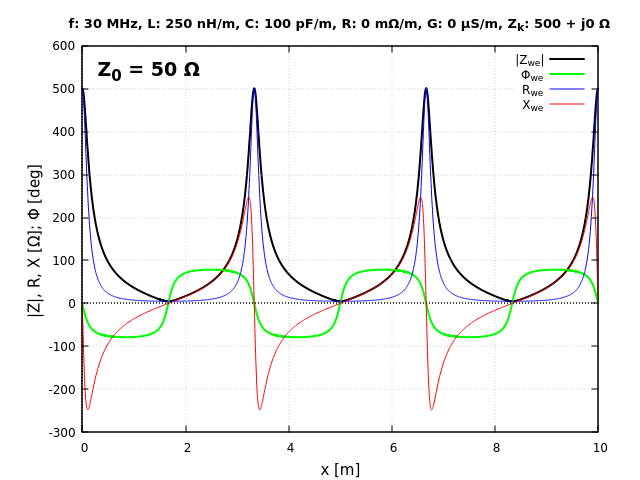
Widzimy, że wykresy uległy jakby pogłębieniu. Powiększmy pierwsze minimum $|Z_\text{we}(x)|$.

Widzimy, że otrzymaliśmy zakres zmian $|Z_\text{we}(x)|$ od $5$ do $500\text{ Ω}$. Potwierdza się zatem wyrażenie (5). Teraz zmniejszmy $Z_\text{k}$ do $25\text{ Ω}$.

Otrzymaliśmy wykresy przesunięte o $\lambda/4$ względem rys. 3. Granice zmian $|Z_\text{we}(x)|$ wynoszą również $25$ i $100\text{ Ω}$ oraz potwierdza się (5).

Rys. 7 podsumowuje dotychczasowe nasze obserwacje w postaci animacji z parametrem $Z_\text{k}$. Przy $Z_\text{k}$ zbliżonym do $Z_0$ impedancja $Z_\text{we}(x)$ reprezentowana jest głównie przez $R_\text{we}(x)$ (wykres niebieski zbliża się do czarnego). Skrajne wartości $Z_\text{k}$ znacznie zbliżają się do klasycznych granicznych przypadków linii długiej zwartej ($Z_\text{k} = 0\text{ Ω}$) i rozwartej na końcu ($Z_\text{k} \rightarrow \infty$). Wówczas przebieg $\mathit{\Phi}_\text{we}(x)$ (zielony) istotnie zbliża się kształtem do prostokątnego $\pm90^\circ$. W wyniku tego zanika $R_\text{we}(x)$ (niebieski) przybierając kształt szpilek, a $X_\text{we}(x)$ zaczyna decydować o całości $Z_\text{we}(x)$ (wykres czerwony przybliża się do czarnego).

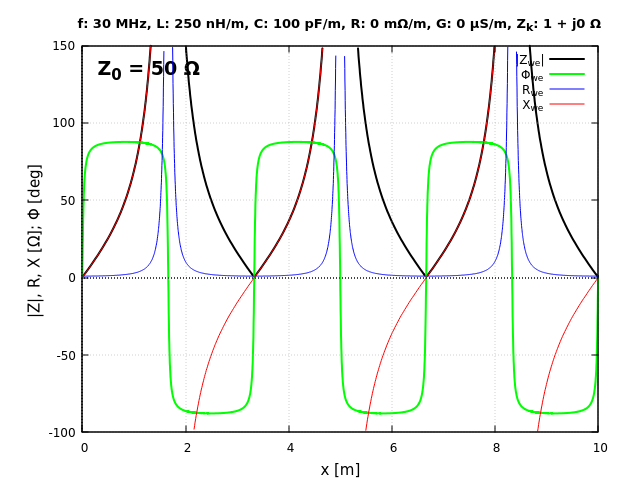
Dotychczas przyjmowaliśmy impedancję obciążenia linii długiej $Z_\text{k} = R_\text{k}$, czyli o charakterze rezystancyjnym ($X_\text{k} = 0\text{ Ω}$). Również założyliśmy linię o rezystancyjnym charakterze impedancji falowej tzn. $Z_0 = R_0$. Zatem równość $|Z_\text{k}| = |Z_0|$ była równoważna $Z_\text{k} = Z_0$, która w prosty sposób wyjaśniała wykres linii prostej na rysunku 2.

Przyjmijmy teraz $Z_\text{k} = 30 + \mathrm{j}40\text{ Ω}$, co przy częstotliwości $30\text{ MHz}$ równoważne jest szeregowemu połączeniu $R_\text{k} = 30\text{ Ω}$ i $L_\text{k} = 212\text{ nH}$. W dalszym ciągu mamy $|Z_\text{k}| = 50\text{ Ω}$, czyli  spełniony warunek $\boldsymbol{|Z_\textbf{k}| = |Z_0|}$. Niestety nie jest spełniona równość $\boldsymbol{Z_\textbf{k} = Z_0}$, zatem o wspomnianej linii prostej mowy być nie może (rys. 8), co wynika wprost z rys. 1a. W tym przypadku to $Z_\text{k}$ możemy określić mianem trudnego obciążenia, ale dla fidera.

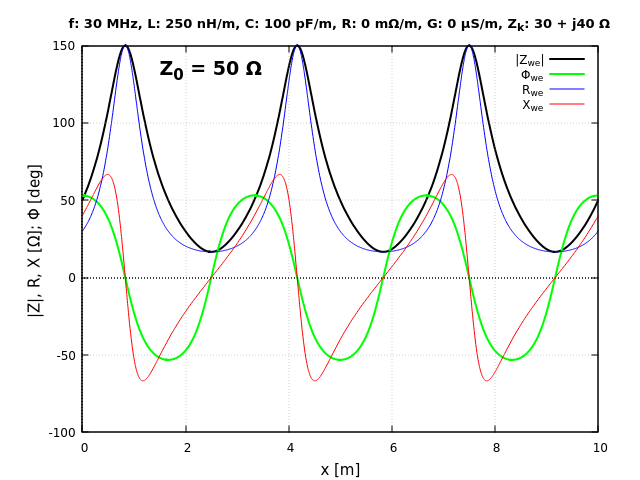
Mamy tu $\mathit{SWR} = 3$, co potwierdza wzór (3). Podobny jak na rys. 8 przypadek wystąpi przy zespolonym charakterze $Z_0$ i rezystancyjnym $Z_\text{k}$.

W szczególności nie zalecam załączania na końcu linii długiej kondensatora o $X_\text{C} = |Z_0|$, bo wtedy przy urojonym obciążeniu ($R_\text{k} = 0\text{ Ω}$) zawsze będzie $\mathit{SWR} \rightarrow \infty$ (odbicie fali w $100\%$), co łatwo zweryfikować wzorami (3).

Również na rys. 8 przy $x$ równym wielokrotności $\lambda/2$ fider wiernie przenosi na swe wejście impedancję obciążenia tzn. zachodzi $Z_\text{we}(n\lambda/2) = Z_\text{k}$. Jesteśmy też w stanie dobrać tak długość $x$ fidera, aby $Z_\text{we}(x)$ miało charakter rezystancji – są to punkty $x$ oddalone od siebie o $\lambda/4$, ale już przesunięte względem końca fidera i punktów np. z rys. 3. Przesunięcie to wynika z fazowego warunku brzegowego, który nakazuje zrównanie się fazy $\mathit{\Phi}_\text{we}(0)$ z fazą $\mathit{\Phi}_\text{k}$. W obu tych przypadkach zmiana długości fidera nie zmienia ani trochę jego fali stojącej – $\mathit{SWR}$ wciąż jest dokładnie równy $3$.

Jak dalej zobaczymy, strojenie anteny do fidera najczęściej polega na realizacji równości $Z_\text{k} = Z_0$ przez zrównanie $R_\text{k} = R_0$ i wyzerowanie $X_\text{k}$. Nie jest to jednak regułą, gdyż istnieją anteny np. FD4, które w swym rezonansie mimo $|Z_\text{k}| = 50\text{ Ω}$ (na zaciskach baluna) mają $X_\text{k} \neq 0\text{ Ω}$, więc stanowią trudne obciążenie. Powoduje to, że zgodnie z rys. 1a taka FD4 zawsze generuje falę stojącą w fiderze (nie mówimy o prądach współbieżnych, to oddzielna kwestia). Prawdopodobnie właśnie przez taką cechę anteny te potocznie nazywane są nierezonansowymi mimo iż np. FD4 faktycznie posiada w swych ramionach rezonans fali identyczny jak w dipolu symetrycznym (na końcach strzałki napięcia, a w środku strzałka prądu).

Trzeba zaznaczyć, że warunek $Z_0 = R_0$ występuje zawsze w linii bezstratnej. Dla linii tej

$$\boxed{Z_0 = \sqrt{L \over C}} \tag{6}$$

Dla linii stratnej warunek ten ma miejsce przy

$$Z_0 = \sqrt{L \over C} = \sqrt{R \over G} \tag{7}$$

W obydwu powyższych przypadkach mamy do czynienia z tzw. linią nie zniekształcającą zdolną do wiernego przenoszenia sygnałów impulsowych np. danych cyfrowych. W celu osiągnięcia (7), często stosuje się sztuczne zwiększenie jednostkowej $L$, a czynność ta nosi nazwę pupinizacji linii (nie dotyczy omawianej tu techniki antenowej). Jednak dalej zobaczymy, że przy dostatecznie małych wartościach $R$ i $G$, zależność (7) nie musi być spełniona.

Linia stratna

Wprowadźmy teraz tłumienie linii równe

$$\boldsymbol{4.3}\text{ dB/100m}$$

Przy założeniu linii nie zniekształcającej (7) daje to

$$R = \boldsymbol{250}\text{ mΩ/m}, \,\, G = \boldsymbol{100}\text{ μS/m}$$

Po obciążeniu takiej linii $Z_\text{k} = Z_0$ otrzymamy linie proste identyczne jak na rys. 2.

Ciekawy przypadek wystąpi w linii stratnej dla $Z_\text{k}$ różnego od $Z_0$, przykładowo dla $Z_\text{k} = 100\text{ Ω}$ (rys. 9).

Jak widzimy, wraz ze wzrostem długości $\boldsymbol{x}$ linii stratnej, $\boldsymbol{Z_\textbf{we}(x)}$ zmierza do $\boldsymbol{Z_0}$. Dzieje się to tym szybciej, im większe jest jednostkowe tłumienie linii. Wynika stąd dla linii stratnej uzależnienie $\boldsymbol{\mathit{SW\!R}}$ od $\boldsymbol{x}$ (zmienna obwiednia z rys. 9), który dla $x \rightarrow \infty$ zmierza do $1$. W istocie, $\mathit{SWR}$ zależy od stosunku amplitud fali odbitej do padającej (współczynnika odbicia $\mathit{\Gamma}$, patrz wzór (3)), a ten dla linii stratnej jest różny w różnych punktach linii [1]. Dla niedopasowania anteny do fidera można więc zapisać $\mathit{SWR}(x > 0) < \mathit{SWR}(0)$.

Jednak korzyść z występowania tłumienia linii jest pozorna, gdyż tracimy też moc. Sytuacja ta jest podobna do zjawisk w antenach zawierających skupione elementy stratne (rezystory) np. T2FD, patrz też zalety i wady Tłumik PI. Zatem w dalszym ciągu kluczowy jest $\mathit{SWR}$ w punkcie $x = 0\text{ m}$ (lub dowolnym $x$ dla linii bezstratnej).

Sprawdźmy jeszcze jaki wpływ na $Z_\text{we}(x)$ linii stratnej ma załączenie wymienionej wyżej $Z_\text{k} = 30 + \mathrm{j}40\text{ Ω}$ ($|Z_\text{k}| = |Z_0| = 50\text{ Ω}$), czyli trudnego obciążenia (rys. 10).

Tu również większe jednostkowe tłumienie i długość linii ma korzystny wpływ na stabilizację $Z_\text{we}(x)$ (zmniejszanie się $\mathit{SWR}$ w miejscu zasilania fidera).

Odniesienie do charakteru $\boldsymbol{Z_0}$

Podsumowując rygorystyczny wymóg $Z_\text{k} = Z_0$ (nie wystarczy równość modułów tych impedancji) należy zauważyć, że:

• Impedancja $\boldsymbol{Z_\textbf{k}}$ na zaciskach anteny (bez fidera) w rezonansie przeważnie ma charakter rezystancji, gdyż pojęcie rezonansu z definicji wiąże się z wzajemną kompensacją wartości $X_\text{L}$ i $X_\text{C}$.
• Impedancja falowa np. przewodów koncentrycznych, w interesującym nas paśmie również ma charakter rezystancji.

Dla uzasadnienia drugiego z powyższych punktów wystarczy przeanalizować wyrażenie (2) na $Z_0$, które przy częstotliwości $30\text{ MHz}$ przybiera postać

$$Z_0 \approx \sqrt{\frac{250 \times 10^{-3} + \mathrm{j}47}{100 \times 10^{-6} + \mathrm{j}19 \times 10^{-3}}} \approx \sqrt{\frac{\mathrm{j}47}{\mathrm{j}19 \times 10^{-3}}} = \sqrt{\frac{47}{19 \times 10^{-3}}} \approx 50 \, \Omega$$

Czyli (6), co powoduje w praktyce nieistotność (7). Zatem nie musimy przyjmować odpowiedniego stosunku $R/G$, by uzyskać $Z_0 = R_0$ i prawdopodobnie fabryki kabli też o ten stosunek nie dbają. Wynika to z faktu, że jednostkowe rezystancja $R$ i konduktancja $G$ są przeważnie dużo mniejsze od jednostkowych odpowiednio reaktancji indukcyjnej $X_\text{L}$ i susceptancji pojemnościowej $B_\text{C}$. Dla wyższych częstotliwości (do pewnej granicy pasma UKF) powyższe przybliżenie staje się jeszcze bardziej dokładne, a więc charakter $Z_0$ jest w większym stopniu czystą rezystancją.

Na wstępie poznaliśmy prosty sposób pomiaru multimetrem jednostkowych: indukcyjności $L$ i pojemności $C$ linii długiej. Teraz wiemy, że możemy skorzystać ze wzoru (6), aby obliczyć jej impedancję falową $Z_0$.

Podsumowanie

Podsumujmy nasze rozważania dla reprezentatywnego fidera mającego impedancje falową $Z_0 = R_0$.

Przy dopasowaniu impedancji obciążenia $Z_\text{k}$ do impedancji falowej fidera $Z_0$ tzn. dla $Z_\text{k} = Z_0$, nie występuje w fiderze fala stojąca tzn. $\mathit{SWR} = 1$. Wówczas impedancja wejściowa fidera $Z_\text{we}(x)$ nie zależy od jego długości $x$ i wynosi $Z_\text{we}(x) = Z_0$. Dla bezstratnej linii długiej jest to równoważne zastąpieniem jej bezpośrednim podłączeniem $Z_\text{k}$ do nadajnika. Krótkofalowiec, który osiągną taki stan dopasowania, nie musi się przejmować jakąkolwiek informacją zawartą w niniejszym artykule :-) Niestety, takie dopasowanie jest trudne do osiągnięcia w szerszym paśmie częstotliwości np. obejmującym chociażby wszystkie amatorskie pasma KF.

Zatem, po naruszeniu powyższego dopasowania, ale przy $X_\text{k} = 0$ (obciąża tylko rezystor $R_\text{k}$), powstaje w fiderze fala stojąca o współczynniku $\mathit{SWR} > 1$ niezależnym od długości $x$ fidera. Jednak $Z_\text{we}(x)$ już zależy od $x$ i ma charakter rezystancji ($X_\text{we} = 0$) przy długościach $x = n\lambda/4$. Zmieniając długość fidera $\boldsymbol{x}$ może zajść albo $\boldsymbol{|Z_\textbf{we}(x)| = |Z_0|}$ albo $\boldsymbol{\mathit{\Phi}_\textbf{we}(x) = 0}$, ale nie obie równości jednocześnie (czyli mamy albo trudne obciążenie albo przeciążenie napięciowe lub prądowe). Zachodzi też $Z_\text{we}(n\lambda/2) = Z_\text{k}$, co z punktu widzenia nadajnika powoduje "zniknięcie" fidera. Fizycznie jednak jest on nadal podłączony mogąc wciąż generować TVI swą falą stojącą. Z punktu widzenia krótkofalowca najistotniejsze jest to, że takie niedopasowanie nie da się już w $\boldsymbol{100\%}$ zniwelować zmianami długości fidera $\boldsymbol{x}$, w szczególności zmiany te nie wpływają na $\mathit{SWR}$. Zmiany $x$ dokonują jedynie częściowego dopasowania $Z_\text{we}(x)$ do $R_\text{nad}$ (modułu albo fazy), które w dalszym etapie można sfinalizować skrzynką antenową dającą docelową równość $Z_\text{we}(x) = R_\text{nad}$.

Jeśli w porównaniu do powyższego będzie $X_\text{k} \neq 0$ (obciążenie zespolone), wnioski będą takie same z ta różnicą, że przesuwamy raster $x$ dających $X_\text{we}(x) = 0\text{ Ω}$ (rezystancję wejściową fidera), ale odległość między tymi $x$ wciąż będzie wynosiła $n\lambda/4$. Dla krótkofalowca oznacza to, że dla każdej wartości $\boldsymbol{Z_\textbf{k}}$ (nawet zespolonej) można dobrać długość $\boldsymbol{x}$ fidera dającą opisane wyżej dwa rodzaje $\boldsymbol{Z_\textbf{we}(x)}$ ze swymi problemami.

Przy niedopasowaniu $Z_\text{k}$ do $Z_0$, w stratnej linii długiej wielkość $\mathit{SWR}$ jest różna w różnych punktach $x$ takiej linii, więc powinno się już oznaczać to jako funkcję $\mathit{SWR}(x)$. Zachodzi wówczas $\mathit{SWR}(x > 0) < \mathit{SWR}(0)$. Przy $x \rightarrow \infty$ wartość $\mathit{SWR}(x)$ zmierza do $1$, a przebieg $Z_\text{we}(x)$ coraz bardziej stabilizuje się na poziomie $Z_0$. Korzyści stosowania przez krótkofalowca linii stratnych (czytaj: wydłużonych) są więc dyskusyjne i podobne do tych w antenach ze skupionymi elementami stratnymi np. T2FD (szerokopasmowość kosztem skuteczności).

W praktyce krótkofalowiec dysponuje najczęściej ograniczonym miejscem na rozwieszenie anteny, więc istotna jest kwestia, jakimi środkami dysponuje dla zbliżenia się do idealnego dopasowania dającego $\mathit{SWR} = 1$. Na przykład możemy zmieniać długość dipola, ale nie za bardzo jego wysokość. Możemy też zmieniać długość fidera, co ułatwia skrzynce zadanie. Często więc wysoki $\mathit{SWR}$ nie wynika z niewiedzy, ale po prostu trudności jego zmniejszenia.

Historia artykułu
2002: powstanie
2014: korekta po przejściu na Joomla (ostatni stat. HTML)
2020-12-30: Wersja 2 (dodanie aspektu fazy)
2023-12-12: korekta podpisów rysunków po przejściu z J3 na J5

Ilustracja wstępna artykułu powstała przy pomocy DALL-E

© Copyright Krzysztof Kolisz SQ8IJZ 2002

Literatura
[1] "Poradnik radio- i teleelektryka. Elementy i podzespoły", Witold Rosiński w pracy zbiorowej pod redakcją Jerzego Antoniewicza, PWT Warszawa 1959.