Wzmacniacz o ujemnej impedancji wyjściowej
Chciałbym zaprezentować bardzo interesujące rozwiązanie wzmacniacza, którego impedancja wyjściowa może przyjmować ujemne wartości (rys. 1).

W układzie tym występuje prądowe szeregowe dodatnie sprzężenie zwrotne. Na wejściu bloku o wzmocnieniu napięciowym $k > 0$ znajduje się sumator napięć. Impedancja wyjściowa $Z_\text{wy}$ tego wzmacniacza wynosi
$$\boxed{Z_\text{wy} = Z_\text{s}(1 - k)} \tag{1}$$
Zatem dla $\boldsymbol{k > 1}$ przyjmuje ona wartości ujemne. Uwidacznia się tutaj ważna funkcja impedancji szeregowej $Z_\text{s}$ – jest ona impedancją prototypową dla osiągnięcia żądanej $Z_\text{wy}$.
Nasuwa się pytanie, po co w ogóle moglibyśmy chcieć posiadać wzmacniacz o ujemnej impedancji wyjściowej? Otóż taki wzmacniacz może mieć ciekawe zastosowanie w audio, w kontekście bezpośredniego zasilania głośnika. Dzięki ujemnej impedancji możemy głośnik zasilać jakby poprzez „tylne drzwi” (back door), omijając $R_\text{DC}$ i/lub $L$ rozproszenia cewki (przynajmniej częściowo). Stwarza to dodatkowe możliwości w porównaniu do zasilania poprzez „oficjalne” zaciski głośnika. Również możemy niwelować rezystancję długich przewodów połączeniowych pomiędzy wzmacniaczem, a kolumną głośnikową.
Przeanalizujmy zatem ten wzmacniacz w kontekście współpracy z pojedynczym głośnikiem (bez zwrotnicy).
Założenia
W praktyce impedancja prototypowa tego wzmacniacza jest reprezentowana przez szeregową gałąź RL lub pojedynczy element R lub L, podobnie jak kompensowane odpowiednie wartości $R$ i $L$ rozproszenia cewki głośnika. Ze względów energetycznych (zasilanie głośnika) wartość $\boldsymbol{Z_\textbf{s}}$ powinna być dostatecznie mała (najwyżej kilka $\%$ wartości $Z_\text{o}$).
Jeśli nie zostanie zaznaczone inaczej, w dalszym ciągu zakładamy
$${\mathrm{Re}Z_\text{o} \over \mathrm{Re}Z_\text{s}} = {\mathrm{Im}Z_\text{o} \over \mathrm{Im}Z_\text{s}} \tag{2}$$
czyli stosunek obu rezystancji jest równy stosunkowi indukcyjności.
Powyższe założenia determinują położenie rozpatrywanych impedancji na jednej prostej w płaszczyźnie zespolonej $R + \mathrm{j}X$. Uprości to analizę stabilności tego wzmacniacza, gdyż nie będziemy musieli badać biegunów jego operatorowej transmitancji (w dziedzinie zmiennej zespolonej $s = \sigma + \mathrm{j}\omega$).
Transmitancja
Wzmocnienie napięciowe $K$ całego wzmacniacza wynosi
$$\boxed{K = {k \over 1 + {Z_\text{s} \over Z_\text{o}}(1 - k)}} \tag{3}$$
Zauważmy, że przy spełnieniu (2) iloraz $Z_\text{s} / Z_\text{o}$ jest liczbą rzeczywistą, a więc też wzmocnienie $K$ całego wzmacniacza. Oznacza to idealnie płaską charakterystykę częstotliwościową tego wzmacniacza (stałe wzmocnienie i zerowa faza). W praktyce nie jest to dokładnie spełnione, gdyż głośniki mają zmienną impedancję w funkcji częstotliwości i przy dużych wartościach wzmocnienia członu $k$ (blisko granicy stabilności) daje się usłyszeć podbarwienia odtwarzanego dźwięku. Mają one charakter średniotonowy, co zostanie za chwilę wyjaśnione.
Jednak równomierny przebieg charakterystyki częstotliwościowej na wyjściu wzmacniacza o ujemnej impedancji wyjściowej nie jest celem samym w sobie. Jeśli bowiem, przykładowo, chcemy skompensować szeregową indukcyjność $L$ dolnoprzepustowego filtra RL tak, by na jego wyjściu (na rezystancji $R$) był równomierny przebieg charakterystyki częstotliwościowej, siłą rzeczy na wyjściu wzmacniacza z rys. 1 zasilającego ten filtr wyższe częstotliwości powinny być wzmacniane bardziej. Wówczas już planowo nie jest spełniona równość (2).
Nasuwa się pytanie, po co w takim razie stosować wzmacniacz o ujemnej impedancji wyjściowej? Czy nie uzyskalibyśmy tego samego zasilając ten filtr RL już skorygowanym częstotliwościowo sygnałem? Otóż, uzyskalibyśmy wówczas korekcję unilateralną (jednostronną, od wzmacniacza do $R$), natomiast wzmacniacz o ujemnej impedancji wyjściowej daje nam korekcję bilateralną (dwustronną, też od $R$ do wzmacniacza, gdyby po stronie $R$ były też jakieś źródła), co ma znaczenie w przypadku hamowania ruchu membrany głośnika, szczególnie przy niwelowaniu jego $R_\text{DC}$.
Szczególną sytuacją w (3) jest wartość $k = 1$ tzn. gdy ten człon wzmacniający jest wtórnikiem. Wówczas niezależnie od wartości $Z_\text{s}$ i $Z_\text{o}$ wzmocnienie całego wzmacniacza również wynosi $K = 1$, a $Z_\text{wy} = 0\text{ Ω}$. Wg. wzoru (1) ta wartość $k$ jest granicą przejścia $Z_\text{wy}$ od dodatnich (dla $k < 1$) do ujemnych wartości impedancji ($k > 1$). Przypadek ten jest odpowiednikiem znanego układu bootstrap.
Stabilność
Dla stabilnej pracy układu wymagane jest spełnienie jednego z dwóch poniższych równoważnych warunków (znaczenie poniższego lewego operatora nierówności zostanie wyjaśnione dalej)
$$Z_\text{wy} + Z_\text{o} > 0 \,\, \Leftrightarrow \,\, k < {Z_\text{o} \over Z_\text{s}} + 1 \tag{4}$$
Z punktu widzenia obciążenia $Z_\text{o}$ obszar stabilnej pracy wzmacniacza jest dla $Z_\text{o} > -Z_\text{wy}$. Przykładowo, jeśli $Z_\text{wy} = -2\text{ Ω}$ (charakter rezystancji), musi być $Z_\text{o} > 2\text{ Ω}$ (wzmacniacz wzbudzi się dla $Z_\text{o} \leq 2\text{ Ω}$). Wynika z powyższego teoretyczna niemożność idealnej kompensacji $\boldsymbol{Z_\textbf{o}}$. Przypominam jednak, że nam chodzi jedynie o kompensację $R$ i/lub $L$ rozproszenia cewki głośnika, a nie całej jego $Z_\text{o}$. Wspomniane wyżej podbarwienia dźwięku mają charakter średniotonowy, gdyż w tym zakresie głośniki miewają najmniejszy moduł impedancji (pomiędzy częstotliwością rezonansową, a przedziałem wpływu indukcyjności cewki głośnika), a więc najbliższy granicy stabilnej pracy wzmacniacza.
Natomiast z punktu widzenia $k$ obszar stabilności to przykładowo $k < 21$, gdy $Z_\text{s}$ stanowi $5\%$ wartości $Z_\text{o}$. Reasumując, ujemna impedancja wyjściowa jest wtedy dla $1 < k < 21$.
Powyżej używaliśmy operatora nierówności ($>$) dla dwóch liczb zespolonych, co nie jest możliwe tak jak to rozumiemy na liczbach rzeczywistych. Jednak przyjmując nasze wstępne założenia (dla głośnika dodatnie $R$ i $X$ oraz równość (2)) poruszamy się nie po całej płaszczyźnie zespolonej impedancji $R + \mathrm{j}X$, a jedynie po prostej przechodzącej przez $0 + \mathrm{j}0$ oraz ćwiartki $\mathrm{I}$ i $\mathrm{III}$ tej płaszczyzny. W takim podzbiorze istnieje porządek: $Z_1 < Z_2$, gdy $\mathrm{Re}(Z_1) < \mathrm{Re}(Z_2)$ (analogicznie na częściach urojonych). Po prostu mamy do czynienia ze zwykłą osią liczbową, ale obróconą w lewo o kąt $\leq 90^\circ$. W granicznych przypadkach jest to oś $R$ (klasyczna oś rzeczywista) lub $\mathrm{j}X$ (prostopadła do niej oś urojona). Ale uwaga, porządek naszego podzbioru impedancji nie jest równoważny porządkowi poprzez moduły. Ten drugi nie uwzględnia bowiem impedancji ujemnych. Przykładowo, w naszym podzbiorze zachodzi $(-2 - \mathrm{j}2) < (1 + \mathrm{j})$, natomiast $|-2 - \mathrm{j}2| > |1 + \mathrm{j}|$.
Praktyczna realizacja
Praktyczna realizacja układu z rys. 1 może polegać np. na dobudowaniu odpowiedniej "przystawki" do posiadanego wzmacniacza audio (rys. 2), który na rys. 1 przejąłby funkcję bloku wzmocnienia $k$ (bez odwracania fazy). Należy wtedy regulację siły głosu tego wzmacniacza ustawić na max, a właściwą regulację $k$ przeprowadzać na jego wejściu (najlepiej bierną). To maksymalne ustawienie siły głosu wzmacniacza audio jest konieczne dla uzyskania możliwości "dopalania" przy starcie lub hamowaniu membrany, bez występowania zjawiska przesterowywania jego stopni wejściowych.
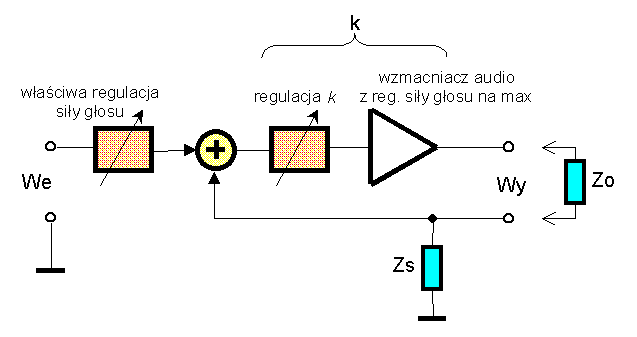
Warto zauważyć, że realizacja ujemnej impedancji wyjściowej jest tożsama z koniecznością zapewnienia rezerwy energetycznej zastosowanego rzeczywistego wzmacniacza m.cz. Przy względnie małej mocy użytkowej dysponujemy dużym zapasem mocy realizując dokładnie ujemną impedancję wyjściową. W praktyce daje się odczuć na słuch istnienie ujemnej $Z_\text{wy}$ już przy $100\%$ rezerwie mocy wzmacniacza w impulsie.
Rozsądnym wydaje się dobudowanie układu zabezpieczającego przed wzbudzaniem. Jednak testując układ np. na głośniku niskotonowym (aktywny subwoofer), zjawisko to dla samego głośnika nie jest szkodliwe.
A jak układ działa w praktyce? Na podstawie własnych doświadczeń zalecam przed uruchamianiem wzmocnienie $k$ sprowadzić do minimum. Następnie stopniowo zwiększać, aż do osiągnięcia charakterystycznej zmiany barwy dźwięku (większy impuls, ale też niestety większe zafalowania charakterystyki częstotliwościowej całego toru wraz z głośnikiem). Dalsze zwiększanie $k$ spowoduje płynne wejście w stan oscylacji. Raz wyregulowany układ działa stabilnie.
Za pomocą tego układu można osiągnąć większe tłumienie membrany głośnika np. niskotonowego, niż przez zwykłe zwarcie jego zacisków (test "pukania" w membranę). Wynika to ze zmniejszenia $Q_\text{TS}$ głośnika poniżej jego wartości znamionowej (podawanej przez producenta). Jest to bardzo efektowny pokaz możliwości wzmacniacza z ujemną impedancją wyjściową.
Historia artykułu
2001: powstanie
2014: korekta po przejściu na Joomla (ostatni stat. HTML)
2023-12-07: korekta po przejściu z J3 na J5
2025-06-23: dodanie wyjaśnień wybranych aspektów
© Copyright Krzysztof Kolisz 2001