Ujemne sprzężenie zwrotne lokalne, czy globalne?
Który rodzaj ujemnego sprzężenia zwrotnego (USZ) we wzmacniaczach audio jest korzystniejszy, sprzężenie lokalne, czy globalne? Niestety nie udzielę tutaj odpowiedzi na to pytanie :-) gdyż każdy z wymienionych rodzajów sprzężeń ma swoje zalety i wady.
Na rys. 1 blok o wzmocnieniu k posiada w rzeczywistości ograniczenia pasma częstotliwości, zarówno od dołu (np. transformator wyjściowy wzmacniacza lampowego, czy kondensatory sprzęgające) jak i od góry (transformator wyjściowy, pojemności wejściowe lamp i tranzystorów). Właśnie ten fakt doprowadza niejednego konstruktora do płaczu ;-)

Stabilność
Obiekt 1-go rzędu, zarówno FDP (filtr dolno-przepustowy) jak i FGP (górnoprzepustowy) wyróżnia się szczególnie od pozostałych filtrów – nie posiada drgań własnych. Ponadto charakteryzuje się tylko jednym parametrem – częstotliwością graniczną. W związku z tym USZ może tylko tę wartość naruszyć. Przykładowo FDP 1-go rzędu ma transmitancję
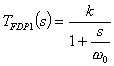 (1)
(1)
gdzie s = jω jest zmienną zespoloną poruszającą się tylko po osi urojonej płaszczyzny zespolonej.
Mamy tutaj przemnożenie wzmocnienia k przez czynnik zależny od częstotliwości (pulsacji ω). Po objęciu takiego filtra pętlą USZ otrzymujemy
 (2)
(2)
czyli również FDP 1-go rzędu, ale o zwiększonej częstotliwości granicznej (pulsacji) w stosunku
![]() (3)
(3)
Tyle samo zmniejszyło się też wzmocnienie. Po załączeniu USZ nie zatraciliśmy podstawowej cechy filtra 1-go rzędu – braku drgań własnych, o czym świadczy nienaruszona w stosunku do nie drgającego (1) postać wyrażenia (2).
Weźmy teraz pod uwagę FDP 2-go rzędu, przykładowo bikwadratowy o transmitancji
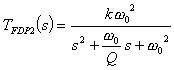 (4)
(4)
Dochodzi tutaj dodatkowy parametr dobroci filtra Q. Trzeba też zaznaczyć, że obiekt ten normalnie posiada drgania własne (gasnące), tym większe im większa wartość Q.
Postępując analogicznie j.w. załączamy USZ, uzyskując transmitancję
 (5)
(5)
Zauważamy, że:
- wzmocnienie spadło 1 + kβ razy,
- tyle samo razy wzrosła dobroć,
- został naruszony współczynnik przy s2 – to już nie jest ten sam obiekt.
Zatem występuje wpływ USZ na każdy parametr tego filtra (podobnie zresztą jak w 1-go rzędu). W praktyce szczególnie dokuczliwy jest wzrost dobroci, powodujący zwiększanie drgań gasnących, a w skrajnych przypadkach – wzbudzenie układu. Te drgania gasnące objawiają się np. w postaci nieczystych wysokich tonów, a w przypadku FGP przewlekłego basu.
Jednak w praktyce mamy do czynienia z obiektami wyższego rzędu o charakterystyce korzystniejszej do współpracy z USZ, niż filtr bikwadratowy. Można je zamodelować np. dwoma stopniami 1-go rzędu o znacznie rozsuniętych częstotliwościach granicznych (biegunach transmitancji).
Z powyższego wynikają następujące zalety lokalnego USZ, obejmującego swym zasięgiem obiekt jedynie 1-go rzędu:
- stabilność,
- "czystość" dźwięku (brak oscylacji gasnących).
Jednak jak się dalej okaże, USZ globalne też ma swojego "asa" w rękawie.
Skuteczność
Przyrównajmy oba rodzaje sprzężeń (rys. 2 i 3).
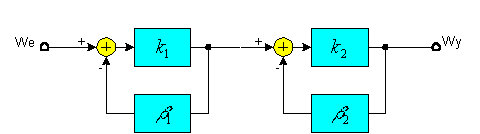

Zakładając równość
![]() (6)
(6)
przedstawiam tabelaryczne porównanie obu rodzajów sprzężeń od We do Wy na rysunkach 2 i 3.
| Parametr | USZ lokalne | USZ globalne | Uwagi |
|---|---|---|---|
| Wzmocnienie | |||
|
Wzmocnienie przy
|
W praktyce przy β < 1 wzmocnienie z globalnym jest mniejsze | ||
|
Wzmocnienie przy
|
1 | 1 | |
|
Krotność zmniejszenia na wyjściu zniekształceń nieliniowych przy
|
Większa skuteczność globalnego |
Tak więc w skrajnym przypadku (podane warunki) skuteczność USZ globalnego jest przy 2 stopniach wzmocnienia k razy większa. Dla n stopni wzmocnienia będzie to przewaga kn−1 krotna nad lokalnym USZ.
Wnioski
Jeśli przyjąć za kryterium porównawcze tylko te wyżej wymienione (a jest ich dużo więcej), można powiedzieć, że:
- sprzężenie lokalne, obejmujące swym zasięgiem obiekt jedynie 1-go rzędu, ma lepsze parametry dynamiczne,
- globalne zachowuje lepsze parametry statyczne.
Historia artykułu
2002-05-27: powstanie
2014: korekta po przejściu na Joomla (ostatni stat. HTML)
2023-12-07: dopiski i korekta po przejściu z J3 na J5
© Copyright Krzysztof Kolisz 2002