Moc prądu zmiennego

W celu przeanalizowania superpozycji mocy dwóch przebiegów napięciowych o różnych częstotliwościach przyjmijmy następującą postać obu tych przebiegów

$$u_1(t) = \sin \left( 2\pi\frac{t}{T_1} \right) \tag{1}$$

$$u_2(t) = \sin \left( 2\pi\frac{t}{T_2} \right) \tag{2}$$

Ich faza początkowa jest identyczna. Pierwszy przebieg wydzieli na rezystancji $1\text{ Ω}$ moc

$$P_1 = \frac{1}{T_1} \int_0^{T_1} \left[ \sin \left( 2\pi\frac{t}{T_1} \right) \right]^2 \mathrm{d}t = \frac{1}{2} \tag{3}$$

Podobnie drugi

$$P_2 = \frac{1}{2} \tag{4}$$

Dalej przyjmuję

$$T_2 = k T_1 \tag{5}$$

Moc całkowita na rezystancji $1\text{ Ω}$ po zsumowaniu obu przebiegów napięciowych, dla okresu $T_2$ wynosi

$$\boxed{P_\text{c}(k) = \frac{1}{kT_1} \int_0^{kT_1} \left[ \sin \left( 2\pi\frac{t}{T_1} \right) + \sin \left( 2\pi\frac{t}{kT_1} \right) \right]^2 \mathrm{d}t} \tag{6}$$

czyli

$$P_\text{c}(k) = 1 + \frac{\sin(2k\pi)}{(k+1)(k-1)\pi} - \frac{\sin(4k\pi)}{8k\pi} \tag{7}$$

Wykres tej funkcji $P_\text{c}(k)$ przedstawiam na rys. 1.

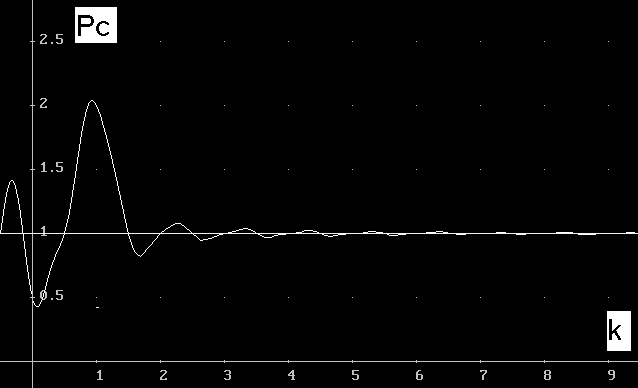
Przypominam o przyjętej jednakowej fazie początkowej obu przebiegów – jest to tutaj istotne, ponieważ w szczególnym przypadku, przy przeciwnych początkowych fazach, dla $k = 1$ uzyskalibyśmy nie zwiększenie, a wyzerowanie mocy.

Z rys. 1 widzimy, że:

• Dla $k = 1$ ($T_2 = T_1$) otrzymujemy moc $2\text{ W}$. Można się było tego spodziewać, gdyż mamy zwykłe podwojenie napięcia przebiegu o tej samej częstotliwości. Moc wtedy wzrasta $4$ razy (z $0.5$ do $2\text{ W}$).
• Dla $k = 1.5, \, 2, \, 2.5, \, 3$ itd. ($T_2$ wzrasta $k$ razy) mamy moc $P_\text{c} = 1\text{ W}$, czyli zwykłą sumę mocy $P_1$ i $P_2$.
• Dla rzeczywistych $k > 1$ mamy oscylacje $P_\text{c}$ wokół $1\text{ W}$ tym mniejsze, im większy stosunek $T$ lub $f$ obu przebiegów. Jest to oczywiste, gdyż dla takiej wartości $k$ przebieg o mniejszym okresie ($T_1$) nie jest całkowany po całym swym okresie. Wynikające z tego zafalowania zanikają dla wystarczająco małego $T_1$, czyli dużego $T_2$ (wyrażanego poprzez $k$). Praktycznie dla $k > 1.5$ amplituda oscylacji nie przekracza $0.2 \cdot (P_1 + P_2)$.

Można odnieść wrażenie "ginięcia" mocy, lecz jej mniejsza wartość na rys. 1 wynika po prostu z niepobierania jej ze źródła.

Dokonując podobnego całkowania jak (6), ale w granicach od $0$ do $10kT_1$

$$P_\text{c}(k) = \frac{1}{10kT_1} \int_0^{10kT_1} \left[ \sin \left( 2\pi\frac{t}{T_1} \right) + \sin \left( 2\pi\frac{t}{kT_1} \right) \right]^2 \mathrm{d}t \tag{8}$$

wyliczamy $P_\text{c}$ za $10$ okresów $T_2$. Otrzymujemy wtedy funkcję, której przebieg przedstawiam na rys. 2.

Zauważamy tutaj wyraźne "zaostrzenie" się zasady superpozycji mocy.

Można też inaczej spojrzeć na problem mocy dwóch przebiegów. Mianowicie zwróćmy uwagę na wyrażenie podlegające całkowaniu we wzorze na $P_\text{c}$. Można je przekształcić do postaci

$$\left[ \sin \left( 2\pi\frac{t}{T_1} \right) + \sin \left( 2\pi\frac{t}{T_2} \right) \right]^2 = \sin \left( 2\pi\frac{t}{T_1} \right)^2 + 2 \sin \left( 2\pi\frac{t}{T_1} \right) \sin \left( 2\pi\frac{t}{T_2} \right) + \sin \left( 2\pi\frac{t}{T_2} \right)^2 \tag{9}$$

Gdyby udało się nam wyeliminować wpływ składnika $2\sin()\sin()$ na wynik całki, mielibyśmy zwykła sumę $P_\text{c} = P_1 + P_2$. Istotnie, składnik ten po scałkowaniu da wartość $0$, jeśli $T_1$ będzie różne od $T_2$ (tutaj pomijam kwestię zafalowania $P_\text{c}$ omówioną powyżej).

Przebieg z rys. 2 przypomina widmo sygnału sinusoidalnego (oś poziomą można wyskalować w częstotliwości $f$). Zachowanie składnika $2\sin()\sin()$ we wzorze (9) leży bowiem u podstaw działania transformacji Fouriera, gdzie jeden z czynników iloczynu (powyżej jest to $\sin()$) jest tzw. jądrem transformacji. W transformacji Fouriera jądrem jest czynnik $\mathrm{e}^{-\mathrm{j}\omega t}$, który pracuje jak wobulator (generator przestrajany).

Historia artykułu
2001: powstanie
2014: korekta po przejściu na Joomla (ostatni stat. HTML)
2023-12-07: dopiski i korekta po przejściu z J3 na J5

© Copyright Krzysztof Kolisz 2001