Wszechprzepustowy transformator szeregowy APTS

Prezentowany układ wszechprzepustowego transformatora szeregowego APTS (all-pass transformer / series, rys. 1) realizuje podział całego pasma częstotliwości na podzakresy, w przypadku APTS2 dolny (niskotonowy) i górny (wysokotonowy), które transformowane są oddzielnie przez każdy z transformatorów składowych. APTS wydaje się konkurencyjny w stosunku do jednego transformatora szerokopasmowego, przy założeniu nie pobierania ujemnego sprzężenia zwrotnego (USZ) zza transformatorów. Pomijając ograniczenia pasma, w istocie układ ten jest bowiem wszechprzepustowym filtrem 1-⁠go rzędu APF1 (all-⁠pass filter), co jest tutaj cechą niepożądaną.

APTS można więc stosować jako transformator w.cz., na przykład antenowy, a nawet transformator wyjściowy wzmacniacza lampowego m.cz. (USZ z anody lampy).

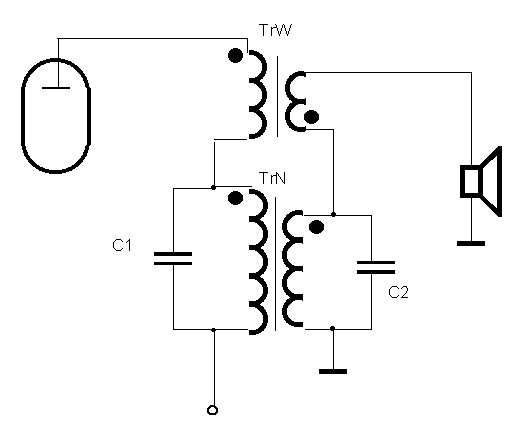
Obecnie przedstawiam jedynie opis teoretyczny, gdyż dotychczasowe praktyczne testy (APTS2) w akustycznym wzmacniaczu lampowym nie były na tyle regularne, aby ich opis można było tutaj zamieścić – zrealizowałem je na dość przypadkowych elementach, a samą ocenę dokonałem na słuch. Wyniki jednak były bardzo zachęcające. Ponadto wykonałem gruntowną symulację komputerową APTS2, która pokazała wszystkie szczegóły i uwarunkowania działania układu.